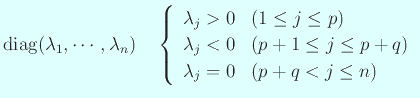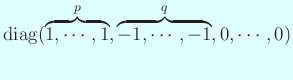


Next: 11.2 見掛けが少し異なる3つの Sylvester の慣性律
Up: 11.1 本題に入る前に
Previous: 11.1 本題に入る前に
-
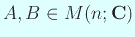 に対して、
に対して、
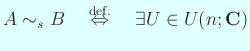
s.t.
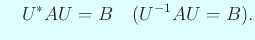
代表元としては Schur 標準形というのか?上三角に出来る
(もとが対称であれば対角行列に出来る)。
実数バージョンもある。
- (今回は関係ない)
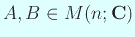 に対して、
に対して、
特異値分解に対応。
-
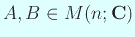 に対して、
に対して、
代表元としては Jordan 標準形が有名。実数の範囲で考えると、
有理標準形とかいうのになる?
「基底の取り替えでなるべく簡単な行列にする」
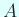 と
と 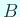 が
が 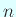 次の実対称行列とするとき、
次の実対称行列とするとき、
代表元として
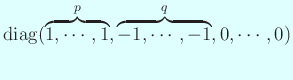 が取れる。
伊理先生は ``Sylvester 形'' と呼んでいた。
これは符号数
が取れる。
伊理先生は ``Sylvester 形'' と呼んでいた。
これは符号数 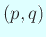 で指定できることに注意。
で指定できることに注意。
「2次形式を正則線形変換で平方完成 (対角化) する」
Hermite 行列版がある。
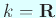 or
or 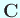 とする。
とする。
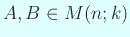 に対して、
に対して、
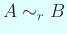
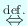
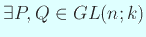 s.t.
s.t. 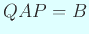 .
.
代表元として
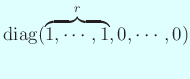 が取れる
(
が取れる
(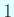 の個数
の個数 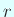 は実は
は実は 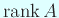 に等しい,
伊理先生はこの代表元を「階数標準形 (rank normal form) と呼んでおく」)。
に等しい,
伊理先生はこの代表元を「階数標準形 (rank normal form) と呼んでおく」)。
実対称行列や Hermite 行列に対して、
直交変換や unitary 変換で相似変換する話は、
1, 3, 4 にまたがっている話になる。
2 はある意味で 1 を緩くしたものである。
3, 4 もある意味で 1 を緩くしたものである。
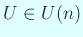 を
を
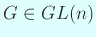 に変えるのだが、そのときに
に変えるのだが、そのときに
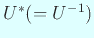 を
を
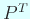 にするか、
にするか、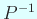 にするか。
にするか。
5 はとても緩い。
例えば実対称行列について、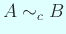
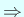
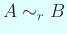 .
.
そうか、実対称行列について、
直交変換に限った 1 (あるいは3) をして、
一般の正則線形変換で 4 をして、
それから 5 をして、
ということで、標準形が、
から
を通じて
となるわけだ。もう
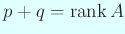 は当たり前に見えて来る。
は当たり前に見えて来る。
書くとすごくゴチャゴチャしている感じがするけれど、
頭の中でやると訳が分からなくなるのは仕方ないのが分かる。
絵的に書くと



Next: 11.2 見掛けが少し異なる3つの Sylvester の慣性律
Up: 11.1 本題に入る前に
Previous: 11.1 本題に入る前に
桂田 祐史
2015-12-22
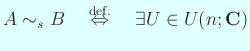 s.t.
s.t.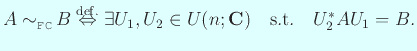
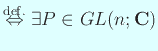 s.t.
s.t.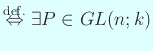 s.t.
s.t.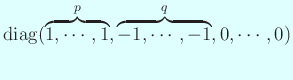 が取れる。
伊理先生は ``Sylvester 形'' と呼んでいた。
これは符号数
が取れる。
伊理先生は ``Sylvester 形'' と呼んでいた。
これは符号数 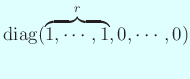 が取れる
(
が取れる
(