Next: 7.4.10 固有値問題 Up: 7.4 Hargreaves [1] の3,4節 Previous: 7.4.8 連立1次方程式
verifynlss() は、“Verified solution of nonlinear system”, つまり非線形方程式の精度保証した解を求める。 アルゴリズムは、Krawczyk 法に基づく (Krawczyk [2], Moore [18])。
![]() ,
,
![]() のとき、
verifynlss(f,xs) とすると、
方程式
のとき、
verifynlss(f,xs) とすると、
方程式
![]() の xs の近くの解を求める。
解の存在が検証できた場合は、解を包み込む区間を返す。
検証できなかった場合は、NaN を返す
1。
の xs の近くの解を求める。
解の存在が検証できた場合は、解を包み込む区間を返す。
検証できなかった場合は、NaN を返す
1。
関数 f が1変数関数の場合、 変数 x の式 f(x) を表す文字列で入力する。
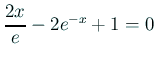 の の |
verifynlss('2*x*exp(-1)-2*exp(-x)+1',1)
|
![]() ,
,
![]() のとき、
verifynlss(f,xs,'h') とすると、
方程式
のとき、
verifynlss(f,xs,'h') とすると、
方程式
![]() の xs の近くの解を求める。
の xs の近くの解を求める。
![]() の場合は、f を定義する M-ファイルを用意する。
の場合は、f を定義する M-ファイルを用意する。
関数の名前は g にするなら
>> edit g |
| 関数 g を定義する M-ファイル g.m |
function y=g(x) y=x y(1)=3*x(1)^2-x(1)+3*x(2)-5; y(2)=4*x(1)+2*x(1)^2+x(2)-7; |
|
|
>> verifynlss(@g,[2,3]) |
intval ans = [ 0.9999, 1.0001] [ 0.9999, 1.0001] |
桂田 祐史