Next: 5 研究の流れ Up: 精度保証ノート Previous: 4 大石「」
![]() は
は
![]() または
または
![]() を表す。
を表す。
複素数
![]() ,
,
![]() (
(
![]() )
に対して、
)
に対して、
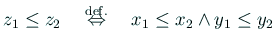
![]()
![]() ,
, ![]() に対して、
に対して、
![]() が区間であるとき、
が区間であるとき、
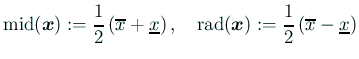
![]() ,
,
![]() ,
, ![]() に対して、
に対して、
![]() の場合は、
の場合は、![]() も
も
![]() も
も
![]() の閉区間を表す。
の閉区間を表す。
![]() の場合は、
の場合は、![]() は複素平面内の
(実軸、虚軸に平行な辺を持つ) 長方形、
は複素平面内の
(実軸、虚軸に平行な辺を持つ) 長方形、
![]() は複素平面内の閉円盤を表す。
は複素平面内の閉円盤を表す。
Rump [5] では、全面的に
![]() を用いている。
を用いている。
![]()
![]()
![]() ,
,
![]() のとき、
区間連立1次方程式
のとき、
区間連立1次方程式
![]() の解集合を次のように定義する。
の解集合を次のように定義する。
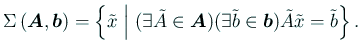
桂田 祐史