


Next: E.1.2.0.3 �$BLdBj�(B8-1
Up: E.1.2 �$BJ?9UE@$H@~7A2=�(B
Previous: E.1.2.0.1 �$BNcBj�(B8-1
�$B$J$s$G%d%3%S9TNs$J$s$+$,=P$FMh$k$N$+!"IT;W5D$K46$8$k?M$,$$$k$+$bCN$l�(B
�$B$^$;$s!#9b9;?t3X$r;W$$=P$9$H!"!VHyJ,$9$k!a@\@~$N79$-$r5a$a$k!J@\@~$r0z�(B
�$B$/!K!W!"$H$$$&4v2?3XE*M}2r$,M-8z$G$7$?!#@\@~$N79$-$rCN$k$@$1$G7k9=?'!9�(B
�$B$J$3$H�(B (�$B4X?t$,$=$3$N6a$/$G�(B 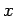 �$B$NA}2C$K$H$b$J$$A}2C$7$F$$$k$N$+!"8:>/�(B
�$B$7$F$$$k$N$+!"6KCM$H$J$C$F$$$k$+Ey�(B)�$B$,J,$+$k$H$$$&$3$H$G$7$?!#6J@~�(B
�$B$NA}2C$K$H$b$J$$A}2C$7$F$$$k$N$+!"8:>/�(B
�$B$7$F$$$k$N$+!"6KCM$H$J$C$F$$$k$+Ey�(B)�$B$,J,$+$k$H$$$&$3$H$G$7$?!#6J@~�(B
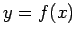 �$B$NE@�(B
�$B$NE@�(B 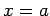 �$B$K$*$1$k@\@~�(B
�$B$K$*$1$k@\@~�(B
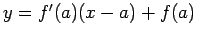 �$B$H$O!"�(B
�$B$H$O!"�(B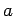 �$B$N6a$/�(B
�$B$G!"�(B
�$B$N6a$/�(B
�$B$G!"�(B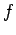 �$B$r�(B1�$B/$78+$(Fq$/$J$j$^$7$?$,!"!VHyJ,$9�(B
�$B$k$H$O�(B1�$Bl9g$N�(B1�$B (
�$B$r�(B1�$B/$78+$(Fq$/$J$j$^$7$?$,!"!VHyJ,$9�(B
�$B$k$H$O�(B1�$Bl9g$N�(B1�$B (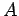 �$B$O9TNs!"�(B
�$B$O9TNs!"�(B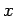 ,
,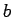 �$B$O%Y%/%H%k$G!"�(B
�$B$O%Y%/%H%k$G!"�(B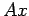 �$B$O9TNs$H%Y%/%H%k$N�(B
�$B$+$1;;$rI=$9�(B)�$B$N7A$N<0$N$3$H$G$9!#$D$^$j�(B
�$B$O9TNs$H%Y%/%H%k$N�(B
�$B$+$1;;$rI=$9�(B)�$B$N7A$N<0$N$3$H$G$9!#$D$^$j�(B 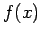 �$B$rE@�(B
�$B$rE@�(B 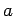 �$B$GHyJ,$7$F!"Hy�(B
�$BJ,78?t�(B(�$B%d%3%S9TNs�(B)�$B$,�(B
�$B$GHyJ,$7$F!"Hy�(B
�$BJ,78?t�(B(�$B%d%3%S9TNs�(B)�$B$,�(B 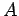 �$B$K$J$C$?$H$$$&$3$H$O!"�(B
�$B$K$J$C$?$H$$$&$3$H$O!"�(B
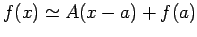 �$B$H9M$($i$l$k!"$H$$$&$3$H$@$C$?$o$1$G$9$M!#�(B
�$B$H9M$($i$l$k!"$H$$$&$3$H$@$C$?$o$1$G$9$M!#�(B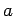 �$B$N6a$/$G$O!"�(B
�$B$N6a$/$G$O!"�(B
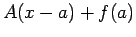 �$B$H$$$&�(B1�$B
�$B$H$$$&�(B1�$B



Next: E.1.2.0.3 �$BLdBj�(B8-1
Up: E.1.2 �$BJ?9UE@$H@~7A2=�(B
Previous: E.1.2.0.1 �$BNcBj�(B8-1
Masashi Katsurada
�$BJ?@.�(B18�$BG/�(B4�$B7n�(B28�$BF|�(B