子供向けの理科の本には素晴らしいものが多い、と思っています 6。 自分が小学生の頃に読んだ
なぜなぜ理科学習漫画 全12巻, 集英社 (19..)など7、 深く印象に残った本が色々あります。 最近見た
ニューワイドずかん百科 科学, 学研 (2006)もなかなか楽しい本です。 その p.47「音をアート作品にする」に目が止まりました。 クラドニ図形 (Chladni figure) の紹介です。 そこには彫刻家である金沢健一氏の不思議な作品 -- それは 正方形や円形をした金属版の上に砂を撒き、 金属版をスーパーボールでこすって振動させることで、 砂が描く不思議なパターンの写真が載っています (「金沢健一」でググると色々ヒットしますので、 お試しを -- いつまで残っているかわかりませんが 1つだけ URL を紹介しておくと、 http://homepage.mac.com/mfukuda2/aiga67/aiga67.html)。 それはクラドニ図形と呼ばれる、という意味のことが書いてありました。
見た瞬間、ラプラシアンの固有関数の ふしのせん節線 (nodal line) であると思いました。
Wikipedia やウィキペディアによると8、 Ernst Florens Friedrich Chladni (1756-1827) は、 ドイツの物理学者で、 (今では当り前に受け入れられている) 隕石が宇宙からやって来ることを唱えたこと、 また音響学への貢献で有名だ、ということです (今回知るまでは全然知りませんでした)。
ネットで検索してみたら、すぐに YouTube に 実験の様子の動画がたくさんアップロードされていることを知りました (例えば ''Sound Waves'')。
Chladni 本人は、1787 年の著作『音響理論の発見』 [2] に、 多くの図版を載せています (http://greg.org/archive/2008/05/28/chladni_figures.html など)。
実験をするのは、残り時間も少ないことだし、 難しいかもしれないと思いましたが、 このような参考データがあるならば卒研テーマにしても大丈夫だろう、 と考えました。
…これを実験テーマにすることに関して、 25年前の私 (院生だった) だったら、 「それはラプラシアンの固有関数の節線であろう、 そういう当り前のことを確認するのはばかばかしい」 と言ったかも知れません。 でも当時先輩から何度もさとされたように、 「やってみないと分からない」 ことがあるものです。実際に学生に取り組んでみてもらって、 現在は「本当に固有関数の節なのかな?」とむしろ疑いも感じるようになっています。 さらに15年さかのぼって小学生の頃の自分に戻ると、 本に書いてあることを確認する実験も嬉嬉としてやっていました (それで時々、意外なことに遭遇しました)。 そういう素朴なノリで数学的なことが出来るのは面白い、と思っています。 学生にとって、ラプラシアンの固有値問題と言うのは、 波動方程式・熱方程式を Fourier の方法で解くために出て来る方便のような ところがあります。 それ自身が我々の眼前に登場しうることを強調してみたいです。
正方形領域
![]() における Dirichlet 境界条件
下の Laplacian
における Dirichlet 境界条件
下の Laplacian
![]() について、
について、
![]() の固有値の重複度については、
以下のことを知識として知っていました。
の固有値の重複度については、
以下のことを知識として知っていました。
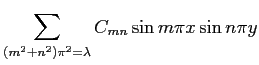
の形をしている。
正方形領域では実のところどうなのか、調べたことはありませんでした。 純粋に整数論的な話であり、有限の範囲ではしらみつぶしで調べられます。 書き捨てのプログラム http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/square-eigenvalue2.cで調べたところ
2 1 :(1,1) 5 2 :(1,2),(2,1) 8 1 :(2,2) 10 2 :(1,3),(3,1) 13 2 :(2,3),(3,2) 17 2 :(1,4),(4,1) 18 1 :(3,3) 20 2 :(2,4),(4,2) 25 2 :(3,4),(4,3) 26 2 :(1,5),(5,1) 29 2 :(2,5),(5,2) 32 1 :(4,4) 34 2 :(3,5),(5,3) 37 2 :(1,6),(6,1) 40 2 :(2,6),(6,2) 41 2 :(4,5),(5,4) 45 2 :(3,6),(6,3) 50 3 :(1,7),(5,5),(7,1) 52 2 :(4,6),(6,4) 53 2 :(2,7),(7,2) 58 2 :(3,7),(7,3) 61 2 :(5,6),(6,5) 65 4 :(1,8),(4,7),(7,4),(8,1) 68 2 :(2,8),(8,2) 72 1 :(6,6) 73 2 :(3,8),(8,3) 74 2 :(5,7),(7,5) 80 2 :(4,8),(8,4) 82 2 :(1,9),(9,1) 85 4 :(2,9),(6,7),(7,6),(9,2) 89 2 :(5,8),(8,5) 90 2 :(3,9),(9,3) 97 2 :(4,9),(9,4) 98 1 :(7,7) 100 2 :(6,8),(8,6) 101 2 :(1,10),(10,1) 104 2 :(2,10),(10,2) 106 2 :(5,9),(9,5) 109 2 :(3,10),(10,3) 113 2 :(7,8),(8,7) 116 2 :(4,10),(10,4) 117 2 :(6,9),(9,6) 122 2 :(1,11),(11,1) 125 4 :(2,11),(5,10),(10,5),(11,2) 128 1 :(8,8) 130 4 :(3,11),(7,9),(9,7),(11,3) 136 2 :(6,10),(10,6) 137 2 :(4,11),(11,4)(以下略) |