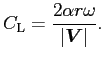

Next: 5.2.2 石川君がやったこと
Up: 5.2 石川雅基『ボールの軌跡』
Previous: 5.2 石川雅基『ボールの軌跡』
理系の人間にとって、
地球表面近くのような一様な重力場のもとで、空気抵抗を無視した場合の、
「投げられた」物体の軌跡については、高等学校の物理でおなじみであろう。
空気を無視しない、つまり抗力・揚力を考慮した場合にどうなるか、
という話である。
と言っても流体力学に本格的に首を突っ込むわけではなくて、
簡単な「公式」を認めて、後は普通の質点の力学の問題とするだけである。
運動する物体が空気から受ける力のうち、
速度方向の成分を抗力 (drag)、
速度と垂直の方向の成分を揚力 (lift) と呼ぶ。
抗力
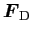 は
は
で与えられる。ここで 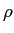 は空気の密度、
は空気の密度、
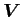 は物体の速度、
は物体の速度、
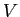 は物体の速さ (
は物体の速さ (
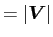 )、
)、
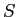 は物体の面積 (
は物体の面積 (
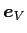 方向の断面積) であり、
方向の断面積) であり、
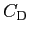 は抗力係数と呼ばれる無次元量である。
は抗力係数と呼ばれる無次元量である。
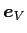 は速度方向の単位ベクトルである。
は速度方向の単位ベクトルである。
これは、初歩の流体力学で学ぶ Stokes の抵抗
1とは異なっている (Stokesの抵抗は、力の大きさが速さに比例しているが、
こちらは速さの自乗に比例している)。
一方、揚力は、2次元の場合は
という式で与えられる。
ここで 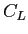 は揚力係数と呼ばれる。
は揚力係数と呼ばれる。
球のような対称性のある物体には、翼のような揚力は生じないが、
回転している場合に、Magnus 力と呼ばれる
揚力
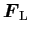 が発生する。
その場合の揚力係数は
が発生する。
その場合の揚力係数は
ここで 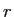 は球の半径、
は球の半径、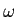 は角速度、
は角速度、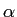 は無次元の定数である。
は無次元の定数である。
ところで [11] のバグ取りを二つ。
- p.?? で抗力を
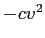 としているが、
としているが、
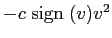 あるいは
あるいは
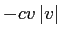 とすべきである。
とすべきである。
- p.?? で
3次元の場合の Magnus 力は、
の形だそうである。ここで
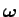 は、
回転の角速度ベクトルである。
は、
回転の角速度ベクトルである。
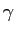 はある比例定数ということであるが、
これについては次項で説明する。
はある比例定数ということであるが、
これについては次項で説明する。


Next: 5.2.2 石川君がやったこと
Up: 5.2 石川雅基『ボールの軌跡』
Previous: 5.2 石川雅基『ボールの軌跡』
桂田 祐史
2015-12-24
![]() は
は
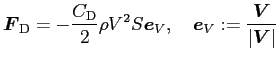
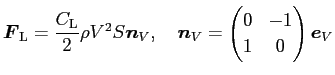
![]() が発生する。
その場合の揚力係数は
が発生する。
その場合の揚力係数は