2.1 はじめに

対数は John Napier (1550-1617) により発見・発明されたことは有名です。 Napier はスコットランドの男爵でしたが、 航海に必要な天文計算に役立てるため、 球面三角法の公式や、数値計算を迅速に行うための対数を発見・発明しました (カジョリ [79])。

図 1: Napier の肖像

図 2: $30^\circ$ 台 ($59^\circ$ 台) の三角関数の対数

既に Napier の主著の一つである Napier [16] の前半部分の 解読は済ませていて、Napier の対数がどういうふうに定義され、 どういう性質を持ち、 どのように利用されるか、ある程度は分かりました (桂田 [17] の「対数の歴史」, 武田 [18], http://sns.math.meiji.ac.jp/?m=pc&a=page_c_home&target_c_commu_id=135)。

数表の１行目を現代の電卓で検算

$$10^7\sin 30^\circ=5000000,$$

$$\mathrm{Nap Log} (10^7 \sin 30^\circ)=10^7\log 2\kinji 6931472,$$

$$\mathrm{Nap Log} (10^7 \tan 30^\circ)=\frac{10^7}{2}\log 3\kinji 5493061,$$

$$\mathrm{Nap Log} (10^7 \sin (90-30)^\circ)= \mathrm{Nap Log} (-10^7 \sec 30^\circ)= 10^7\log\frac{2}{\sqrt{3}} \kinji 1438410,$$

$$10^7\sin(90-30)^\circ=10^7\sin 59^\circ60'=\frac{10^7}{2}\sqrt{3} \kinji 8660254.$$

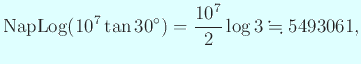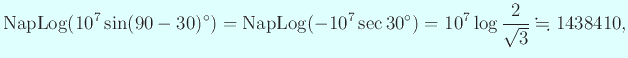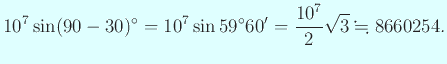(なお現代人にとって $\sin(90-30)^\circ=\cos 30^\circ$ であるが、 この時代、三角比と言えば、$\sin$ , $\tan$ , $\sec$ のことで、 余角の $\sin$ , $\tan$ , $\sec$ である $\cos$ , $\cot$ , $\cosec$ というものは、 そもそも言葉がなかったことに注意。 Napier は $\mathrm{Nap Log}(10^7\sin(90-30)^\circ)$ は $-\mathrm{NapLog}(10^7\sec30^\circ)$ に等しいということは分かっていた。 一つ注意しておくと、まだ小数が普及していなかった時代だが (そもそも小数点の記号 $.$ は Napier の発案だとか)、 負の数は既に普及していた。)

数表を記憶している人にはおなじみの、 $\log 2=0.6931472\cdots$ が見える。 $e$ の値そのものはないけれど、自然対数の値はちらりと見えるわけです。