Next: 2.3 今後の課題 Up: 2 Napier による対数関数の計算 Previous: 2.1 はじめに
手短にまとめると、 Napier は、現代の理工学者ならば微分方程式を使うに違いないような、 仮想的な運動により対数を定義しました。 (Napier はガリレオとほぼ同時代人で、 微積分が存在しない時代に活躍した人なので、 時代を超越したことをやり遂げたように思われます)、
|
|
![\includegraphics[width=12cm]{eps/napierlog.eps}](img34.png)
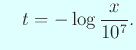
一方
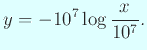 ゆえに
ゆえに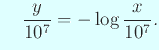
つまり Napier の対数を
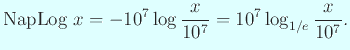
しばしば、Napier の対数は底が
Napier は20年かけて数値計算することで対数表 (正確に言うと、
7桁精度の三角関数の対数の表) を作成しました。
![]() による乗除算があるのは、小数を避けるための工夫です。
による乗除算があるのは、小数を避けるための工夫です。
桂田 祐史