- ...
�$B$+$i�(B1
- �$BGHF0J}Dx<04X78$N%W%m%0%i%`$O!"�(B
�$B$+$J$j2<$NJ}$K$"$j$^$9!#�(B
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... �$B$H8F$P$l$k�(B2
- �$BG.J}Dx<0$N>l�(B
�$B9g$HF1MM$K!"GHF0J}Dx<0$K$b6u4V�(B 2 �$B.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... �$B$G$"$k$H$7$F07$&�(B3
- �$B$3$N$h$&$J�(B
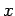 ,
, 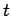 �$B$NC10L$NJQ49�(B
�$B!J?t3XE*$K$OJQ?t$N0l.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
�$B$NC10L$NJQ49�(B
�$B!J?t3XE*$K$OJQ?t$N0l.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
�$B$,F@$i$l$k�(B4
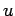 �$B$NE@�(B
�$B$NE@�(B 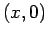 �$B$K$*$1$k�(B
�$B$K$*$1$k�(B 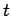 �$B$K$D$$$F$NE83+�(B
�$B$K$D$$$F$NE83+�(B
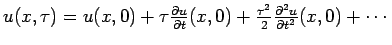 �$B$K$*$$$F!"4X78<0�(B
�$B$K$*$$$F!"4X78<0�(B
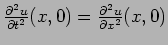 �$B$,@.N)$9$k$H$7$F!"$3$N�(B
�$B$,@.N)$9$k$H$7$F!"$3$N�(B
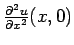 �$B$r�(B
�$B$r�(B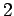 �$B3,Cf�(B
�$B?4:9J,>&$G6a;w$7$?!#�(B
�$B3,Cf�(B
�$B?4:9J,>&$G6a;w$7$?!#�(B
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.