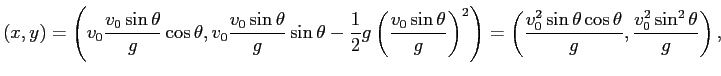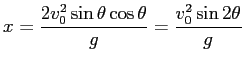

Next: 3 Mathematica の DSolve[]
Up: 2 微分方程式ことはじめ
Previous: 2.1 自由落下 (free fall)
2.2 放物運動 (projectile motion, parabolic motion of projectiles)
物を投げたときの運動を考える。
鉛直上向きに 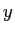 軸を取り、
投げる方向の水平方向に
軸を取り、
投げる方向の水平方向に 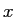 軸を取ると
(やや苦しい説明…)、
軸を取ると
(やや苦しい説明…)、
|
(1) |
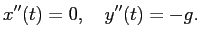 |
最初 (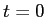 ) の位置を
) の位置を 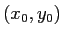 ,
投げる速さを
,
投げる速さを 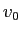 ,
投げ上げる角度を (地面から測った角度で)
,
投げ上げる角度を (地面から測った角度で) 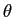 (
(
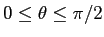 )とすると、
)とすると、
|
(2) |
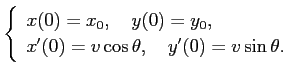 |
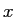 と
と 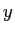 , 2つあって難しいようだけど、
, 2つあって難しいようだけど、
と並べ直してみると、実は両者は独立で、
それぞれ上で説明した型の問題で、難しくなく解ける:
|
(3) |
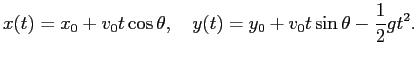 |
簡単のため 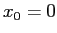 ,
, 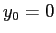 とすると
とすると
(後で、一般の場合の結果が欲しければ、
結果の 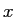 ,
, 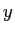 をそれぞれ
をそれぞれ 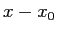 ,
, 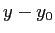 で置き換えればよい。)
で置き換えればよい。)
 の場合は、
の場合は、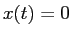 ,
,
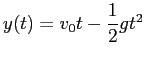 .
.
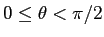 とすると、
最初の式から
とすると、
最初の式から
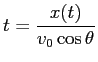 .
これを第2式に代入して
.
これを第2式に代入して
という軌跡の方程式が得られる。
簡単のため、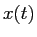 ,
, 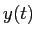 をそれぞれ
をそれぞれ 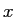 ,
, 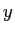 で表し、
平方完成の式変形をすると
で表し、
平方完成の式変形をすると
ゆえに、軌跡は軸が
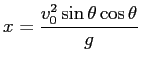 ,
頂点が
,
頂点が
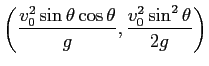 , 下開きの放物線である。
最高の高さは
, 下開きの放物線である。
最高の高さは
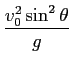 .
これは
.
これは
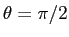 のときに最大になる
(というのは、
のときに最大になる
(というのは、
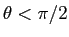 として議論しているので実は乱暴である)。
として議論しているので実は乱暴である)。
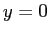 となるのは、
となるのは、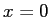 (これは明らか) と
(これは明らか) と
これが地面に落ちる場所を表している。
高校物理の暗記術としては、
最高点に到達する時刻は
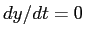 から
から
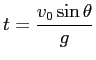 ,
その位置は
,
その位置は
地面に落ちるには、最高点に到達するのに要する時間の2倍かかるとして、
その場所は
という求め方をする。軌跡が放物線であることは、
ある意味ズルして覚えておくわけだ。 


Next: 3 Mathematica の DSolve[]
Up: 2 微分方程式ことはじめ
Previous: 2.1 自由落下 (free fall)
桂田 祐史
2013-07-14
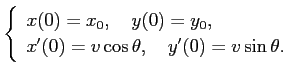
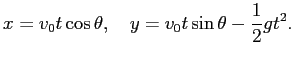
![]() の場合は、
の場合は、![]() ,
,
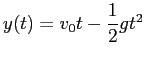 .
.
![]() とすると、
最初の式から
とすると、
最初の式から
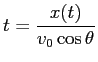 .
これを第2式に代入して
.
これを第2式に代入して
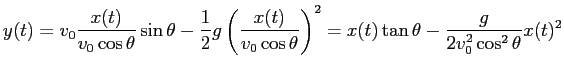
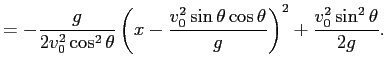
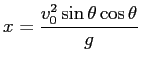 ,
頂点が
,
頂点が
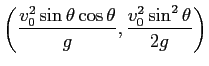 , 下開きの放物線である。
最高の高さは
, 下開きの放物線である。
最高の高さは
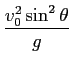 .
これは
.
これは
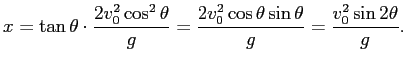
![]() から
から
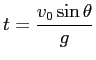 ,
その位置は
,
その位置は