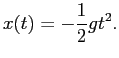

Next: 2.2 放物運動 (projectile motion,
Up: 2 微分方程式ことはじめ
Previous: 2 微分方程式ことはじめ
時刻 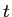 における高さを
における高さを 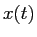 とする。
1階微分
とする。
1階微分 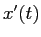 が速度、
2階微分
が速度、
2階微分 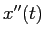 が加速度である。
物理学では、重力による加速度は下向きに大きさ
が加速度である。
物理学では、重力による加速度は下向きに大きさ 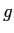 (重力加速度と呼ばれる定数、
SI単位系でほぼ
(重力加速度と呼ばれる定数、
SI単位系でほぼ
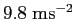 ) であると言われている。
) であると言われている。
この解は (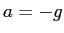 というだけだから)
というだけだから)
例えば最初 (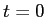 ) に高さ 0
, 速度 0
だったとすると、
) に高さ 0
, 速度 0
だったとすると、
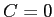 ,
, 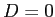 であることが分るので、
であることが分るので、
この場合、時刻 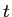 での速度
での速度 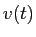 は、
は、
以上の事実は、有名なガリレオ・ガリレイ (Galileo Galilei,
1564-1642) が明らかにしたが、
微積分がまだなかったので非常に苦労した。 


Next: 2.2 放物運動 (projectile motion,
Up: 2 微分方程式ことはじめ
Previous: 2 微分方程式ことはじめ
桂田 祐史
2013-07-14
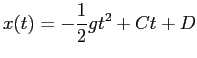 (
(