A..2.1 $\arctan$ の Taylor 展開を用いて計算する

既に言ってあるように、

http://nalab.mind.meiji.ac.jp/~mk/syori2-2013/jouhousyori2-2013-08/node7.html

で紹介した piarctan.BAS が叩き台になる。 これは、与えられた $N$ に対して、

$$\tan^{-1} x=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{2n-1}x^{2n-1} \vert x\vert<1$$ (1)

にやや強引に¹ $x=1$ を代入した

$$\frac{\pi}{4}=\tan^{-1} 1=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{2n-1} =1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$ (2)

の右辺の級数の第 $N$ 部分和 $S_N$ を計算するプログラムである。

piarctan.BAS (再掲)

REM piarctan.BAS --- マーダヴァ・グレゴリー・ライプニッツ級数でπを計算
REM arctan 1 の級数を第 n 項まで計算
REM 次の行は最初 INPUT X としてあったのを修正しました
X=1
INPUT N
F=-X*X
T=X
S=0
FOR J=1 TO N
  A=T/(2*J-1)
  S=S+A
  T=F*T
NEXT J
PRINT "arctan(x)≒";S
PRINT "その4倍";4*S
REM 組込み定数 PI との差を計算してみる
PRINT USING "πとの差=-%.###^^^^^^";4*S-PI
END

この (2) は有名であるが、収束は非常に遅い。 実際、実験で容易に確認できるように

$$\pi-4S_N\kinji \frac{1}{N}$$

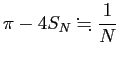
が成り立つ (1億($=10^8$ )項足して、誤差 $10^{-8}$ -- $10$ 桁も合わない)。 どんなにコンピューターの計算が速くても、 $100$ 桁の精度の値を計算するのは無理である。

しかし、これは $x$ の値として、収束ギリギリの $x=1$ を代入するからである (繰り返しになるが、 (1) の収束半径は $1$ であり, 冪級数は収束円の内部では必ず収束するが、 円周上の点で収束するかどうかは case by case で、 収束しても「遅い」場合が多い)。 $\vert x\vert<1$ なる $x$ に対しては、 (1) の収束はぐっと速くなる。

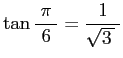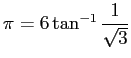一番簡単なのは、高校生でも分かる $\tan\dfrac{\;\pi\;}{6}=\dfrac{1}{\sqrt{3 }\;}$ に基づく、 $\pi=6\tan^{-1}\dfrac{1}{\sqrt{3}}$ を用いることである。

X=1 を X=1/SQR(3) に変え、 $4$ をかけるところを $6$ をかけるように変えたものが次のプログラムである (OPTION ARITHMETIC DECIMAL_HIGH にも変えた)。

kadai8b1.BAS

REM kadai8b1.BAS --- マーダヴァ・グレゴリー・ライプニッツ級数でπを計算
REM arctan(1/√3) の級数を第N項まで計算
OPTION ARITHMETIC decimal_high
INPUT N
LET X=1/SQR(3)
LET F=-X*X
LET T=X
LET S=0
FOR J=1 TO N
   LET A=T/(2*J-1)
   LET S=S+A
   LET T=F*T
NEXT J
PRINT "6*arctan(x)≒";6*S
REM 組込み定数 PI との差を計算してみる
PRINT USING "πとの差=-%.###^^^^^^":6*S-PI
END

最後に PI と比較しているのは、 カンニングであるが (苦笑)、 その結果は次のようになり、 $N=210$ くらいで $100$ 桁精度を実現しているようである (差が大体 $3.9\times10^{-103}$ であるから)。

kadai8b1.TXT ($N=210$ の場合)

? 210
6*arctan(x)≒ 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798175415515142074668914143478172519579252999001468666117910963800249473594922589558451149412426597243798192135258779349163444188419002776980473968671998254815310845772183661993477117122206330295980300468265032425044971769581966122368923975830190359265260280452439469056239411353322600285365354079198623561329837112540037802583883742612430308012431266108485579200748300447615517051621776071743812297241593061362796460193924590409288715907812776745710640173447366147858476628929330128224069043383756471261001339104089689573643179485746003276589222538648739794448220503879861605852796470434461563725003377966770398821962936563887508996436649003257909678486654464777327912490175223366294675627953729664047127912971230253567836505483256602936448002590856734658997052628800136082809703995747012631975584920533663300884564944271834022542189687366731857503436221868148525708031224234008111518938525225632668655196746 
πとの差=-3.939E-0103

$N$ が増加するにつれて、精度がどのように上がっていくか見るために、 INPUT N をやめて、 全体を

FOR N=10 TO 210 STEP 10
...
NEXT N

と FOR NEXT ループにして、次の表 9 の結果を得る。

図 9: 項数 $N$ と誤差

$N$	誤差
$10$	$-2.143\times 10^{-6}$
$20$	$-1.839\times 10^{-11}$
$30$	$-2.085\times 10^{-16}$
$40$	$-2.654\times 10^{-21}$
$50$	$-3.601\times 10^{-26}$
$60$	$-5.086\times 10^{-31}$
$70$	$-7.387\times 10^{-36}$
$80$	$-1.095\times 10^{-40}$
$90$	$-1.649\times 10^{-45}$
$100$	$-2.514\times 10^{-50}$
$110$	$-3.872\times 10^{-55}$
$120$	$-6.011\times 10^{-60}$
$130$	$-9.399\times 10^{-65}$
$140$	$-1.478\times 10^{-69}$
$150$	$-2.337\times 10^{-74}$
$160$	$-3.710\times 10^{-79}$
$170$	$-5.915\times 10^{-84}$
$180$	$-9.461\times 10^{-89}$
$190$	$-1.518\times 10^{-93}$
$200$	$-2.442\times 10^{-98}$
$210$	$-3.939\times 10^{-103}$

図 10: 項数 $N$ と誤差 (縦軸対数目盛)

誤差が大体等比数列的に ($N$ に関して指数関数的に？) 0 に収束している様子が 分かる 本当はこういうのはグラフにするのが良い。 ここでは gnuplot (1年生のときに習ったはず) を使ってみたが、 もちろん十進 BASIC で描くのも簡単である。

それでは、要求されていた結果を求めるプログラムを作ろう。 課題2Bでやったように、FOR NEXT で N を大きくして行って、 部分和を計算するプログラムにする。

kadai8b2.BAS

REM kadai6b2.BAS --- マーダヴァ・グレゴリー・ライプニッツ級数でπを計算
REM arctan(1/√3) の級数を10,20,...,250項まで計算
REM 結果は小数点以下110位まで表示
OPTION ARITHMETIC decimal_high
LET FMT$="N=### -%."&REPEAT$("#",110)
LET N=250
LET X=1/SQR(3)
LET F=-X*X
LET T=X
LET S=0
FOR J=1 TO N
   LET A=T/(2*J-1)
   LET S=S+A
   LET T=F*T
   IF MOD(J , 10) =0 THEN
      PRINT USING fmt$:J,6*S
   END IF
NEXT J
REM 組込み定数 PI との差を計算してみる
PRINT USING "πとの差=-%.###^^^^^^":PI-6*S
END

結果は次のようになる (TEX で \scriptsize コマンドを使って縮小)。

N= 10  3.14159051093808009964275422994425504368823543729459863385301608264097243139275244243408049537664837144194195965
N= 20  3.14159265357140338177371056457791845749708370902558800062450336039110974863967354187227900363909324495379551167
N= 30  3.14159265358979302993126907675698512128890364163387594078160677223250316907504141910094384327780556430672531665
N= 40  3.14159265358979323845998904545815723164682333580898559851810755021711576515774234507828600074005410050567590231
N= 50  3.14159265358979323846264334727215223712766242383933328994947074253583407491260142245980404128750279799354137185
N= 60  3.14159265358979323846264338327899429478611788675967126248193958028428440424653148715465478961463146251880103922
N= 70  3.14159265358979323846264338327950287681011408881114209344980232821142119403271477392517560945005206755050370174
N= 80  3.14159265358979323846264338327950288419705988682105507083891588023987499387955321296887381276928532730590072263
N= 90  3.14159265358979323846264338327950288419716939772598750958858556364736336671762754275139106652717651497248200692
N=100  3.14159265358979323846264338327950288419716939937508067873446993355312916323675359893283010326258393751533470850
N=110  3.14159265358979323846264338327950288419716939937510582058777735023191320405347993715459391151728912750033891584
N=120  3.14159265358979323846264338327950288419716939937510582097493858083854337957828522717360102517299756190923350247
N=130  3.14159265358979323846264338327950288419716939937510582097494459221382757184428319165349115190289161510116917782
N=140  3.14159265358979323846264338327950288419716939937510582097494459230781492806566013451682112808110943615477604646
N=150  3.14159265358979323846264338327950288419716939937510582097494459230781640626284131806763014633707611386690905481
N=160  3.14159265358979323846264338327950288419716939937510582097494459230781640628620862758871391779973144580812870063
N=170  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862212031675396342638517754282
N=180  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803473073620684479093638320
N=190  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534059912106400090011
N=200  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211704355929502943
N=210  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798175415515
N=220  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808014
N=230  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651
N=240  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651
N=250  3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651
πとの差= 2.722E-0122

少々字が小さくて見づらいが、 $N=230,240,250$ の場合に、 小数点以下$110$ 位までの小数表示が一致していることが分かる。 これで小数点以下$100$ 位までの値は得られていると考えて良いだろう。

円周率 $\pi$ の小数点以下 $110$ 位まで

 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510
   58209 74944 59230 78164 06286 20899 86280 34825 34211 70679
   82148 08651

(要求されていたのは、$100$ 位までだったが、$101$ 位が `8' で、 四捨五入を考えると微妙なので、$110$ 位まで表示しておく。)

100桁の数をそのまま表示されても読みづらいので、 10あるいは5桁ごとにブランクをいれるなどすると親切であろう。 なお、筆者自身はそれを「手で」行ったが、 過去に十進 BASIC にやらせた学生もいた (感心しました)。

(参考) pi100.BAS 5桁ずつ区切って表示

OPTION ARITHMETIC decimal_high
LET FMT$="%."&REPEAT$("#",110)
LET PI100$=USING$(fmt$,PI)
PRINT "3."
FOR i=0 TO 20
   PRINT mid$(PI100$,i*5+3,5)&" ";
   IF MOD(i,10)=9 THEN
      PRINT
   END if
NEXT i
END

pi100.TXT

3.
14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 
58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 
82148