2.5 $\tan^{-1}x$ ($\arctan x$ ) のテイラー級数で $\pi$ を計算しよう

円周率 $\pi$ は、例えば

$$\pi =4\arctan 1 \Iff \tan\dfrac{\pi}{4}=1 ,$$

$$\pi =6\arctan \frac{1}{\sqrt{3}} \Iff \tan\dfrac{\pi}{6}=\dfrac{1}{\sqrt{3}}$$

のように $\arctan$ を用いて表すことが出来ます。 $\arctan$ の値をテイラー級数として計算すれば、 円周率の計算法が得られるわけです (それぞれ、マーダヴァ・グレゴリー・ライプニッツ級数, シャープの級数と呼ばれます)。

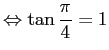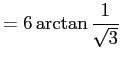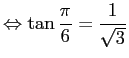テイラー級数の計算では、 級数の一般項の計算に漸化式を用いるのが便利なことが多いです ³(先ほどの $\exp$ のプログラムを思い出して下さい、 実はこの $\arctan$ については「それほど便利でもない」かもしれませんが…)。

$\arctan$ のテイラー展開

$$\arctan x=\sum_{n=0}^\infty \frac{(-1)^{n-1}}{2n-1}x^{2n-1} =\lim_{n\to\infty}\sum_{j=0}^n \frac{(-1)^{j-1}}{2j-1}x^{2j-1}$$

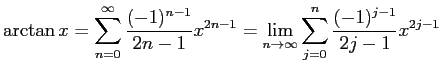
については、一般項は

$$a_j=\frac{(-1)^{j-1}}{2j-1}x^{2j-1}.$$

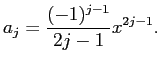
この $a_n$ そのものの漸化式はあまり計算に便利ではありませんが、

$$t_j:=(-1)^{j-1}x^{2j-1}$$

とおくと、$t_j$ は簡単な漸化式

$$t_1=x,\quad t_{j}=- x^2 t_{j-1}$$

を用いて計算でき、$a_j$ は

$$a_j=\frac{t_j}{2j-1}$$

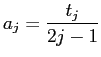
で計算できます。 そこで次のようなプログラムを得られます。

piarctan.bas

REM piarctan.BAS --- マーダヴァ・グレゴリー・ライプニッツ級数でπを計算
REM arctan 1 の級数を第 n 項まで計算
REM 次の行は最初 INPUT X としてあったのを修正しました
X=1
INPUT N
F=-X*X
T=X
S=0
FOR J=1 TO N
  A=T/(2*J-1)
  S=S+A
  T=F*T
NEXT J
PRINT "arctan(x)≒";S
PRINT "その4倍";4*S
REM 組込み定数 PI との差を計算してみる
PRINT USING "πとの差=-%.###^^^^^^";4*S-PI
END

このプログラムでは、

$$\pi=4\arctan 1=4\left(1-\frac{1}{3}+\frac{1}{5}-\cdots\right)$$

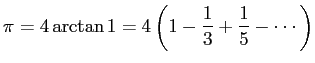
という級数の第 $n$ 項までの和を計算して、表示しています。

また、十進BASICでは、PI という名前で円周率の値が得られるので、 それを利用して誤差も表示しています。

結果は次のようになります。

$n$	$4 s_n$
$10$	$3.04183961\cdots$
$100$	$3.13159290\cdots$
$1000$	$3.1405926538\cdots$
極限	$3.1415926535\cdots$

$\pi=3.14159265358979323846\cdots$ との一致具合いはどうでしょうか？ (誤差⁴は どれくらいでしょうか) 不思議なことに気付いた人、 もしその理由が分かったら、 レポートを書いて送って下さい。