2.6 レポート課題8B

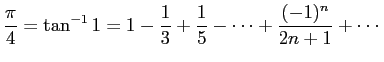
piarctan.BAS は、 マーダヴァ・ゴレゴリー・ライプニッツ級数

$$\frac{\pi}{4} =\tan^{-1} 1 =1-\frac{1}{3}+\frac{1}{5}-\cdots+\frac{(-1)^n}{2n+1}+\cdots$$

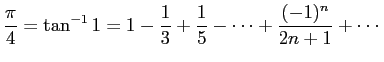
に基づいていて、一応円周率の計算は出来るのですが、 極限値に近づくのがかなり遅く、 $1000$ までの和を計算しても 小数点以下第3位のところで食い違いが出てしまいます。

少し工夫して (具体的には、付録 (例えば A.2.2) にある公式のどれかを使って)、 円周率の値 1000 桁を求めて下さい。

一番安直には、シャープの級数

$$\frac{\pi}{6}=\tan^{-1}\frac{1}{\sqrt{3}} =\frac{1}{\sqrt{3}}-\f... ...{5}\cdot\frac{1}{3^2\sqrt{3}} -\frac{1}{7}\cdot\frac{1}{3^3\sqrt{3}} +\cdots$$

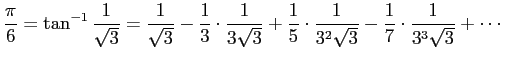
を用いる、という手があります。 一般項が 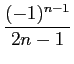$\dfrac{(-1)^{n-1}}{2n-1}$ から、 $\dfrac{(-1)^{n-1}}{2n-1}x^{2n-1}$ ( $x=1/\sqrt{3}$ ) になったことで、 格段に速く極限値に近づきます。

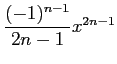100位まで計算する場合と、1000位まで計算する場合で、 計算の手間 (加える項の数がいくつ必要か等) がどれくらい違うかを調べて下さい (計算結果そのものは50位までレポートに記せば良いです)。 出来れば、前節の piarctan.BAS (マーダヴァ・グレゴリー・ライプニッツ級数で計算する) との比較もして下さい。

$\arctan$ 型の公式を使う場合は、 (当然) 上のプログラム piarctan.BAS がたたき台となるでしょう。

テイラー級数による公式でなく、 AGM 公式を使うのは案外プログラミングが簡単かもしれません (AGM公式の背景を理解するのは難しいですが…)。

選んだ方法 (公式)、 計算に用いた BASICプログラムとその簡単な説明、 そのプログラムの実行結果、 簡単な分析を含んだ文書 kadai8b.pdf を作成し、 Oh-o! Meiji で送って下さい。 締め切りは 6月18日 (火曜) 18:00 とします。