A..2.2 逆三角関数のテイラー展開を用いる方法

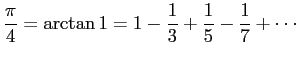円周率を逆三角関数の値を元にして表現し、 逆三角関数をテイラー展開で計算するという公式が現れました。 有名なものは、 「グレゴリー級数」または「ライプニッツ級数」とも呼ばれる

$$\frac{\pi}{4} =\arctan 1 =1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$ (1)

です。これは

$$\arctan x=\sum_{n=1}^\infty \frac{(-1)^{n-1}}{2n-1}x^{2n-1} \mbox{($\vert x\vert<1$)}$$ (2)

を基礎としているわけですね⁷。

この (2) は、 現在の数学のカリキュラムでは、 微積分を用いて、 いわゆる Taylor 展開

$$f(x)=\sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x-a)^n$$

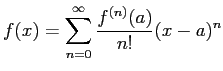
として理解するのが普通ですが、 驚いたことに微積分がなかった 1400 年頃のインドで発見されていた (発見者はマーダヴァという名前だとか) ことが分かっています。

余談

$\arctan$ の計算には

$$\arctan x=\frac{y}{x}\left(1+\frac{2}{3}y+\frac{2\cdot 4}{3\cdot 5}y^2+ \cdots\right),\quad y=\frac{x^2}{1+x^2}$$

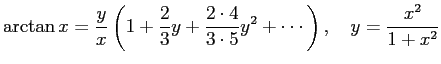
も使われた (L. Euler が使ったのが有名)。

    また Newton が発見した

$$\arcsin x=x+\frac{1}{2}\frac{x^3}{3} +\frac{1\cdot 3}{2\cdot 4}\frac{x^5}{5} +\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\frac{x^7}{7}+\cdots$$

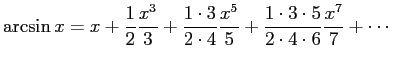
も利用できる。

     なお $\arcsin^2$ の展開

$$(\arcsin x)^2=2\sum_{n=0}^\infty\frac{(n!2^n)^2}{(2n+2)!}x^{2n+2}$$

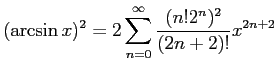
は Euler の 1737 年の発見ということになっているが、 江戸時代の和算家たけべかたひろ建部賢弘の 1722 年のてつじゅつさんけい綴術算経に載っている。

実は (7) は、 収束が遅すぎて (項数を非常に大きく取らないと良い近似値が得られない) 実用的ではありませんが、

もっと小さな $x$ の $\arctan$ を用いるとかなり実用的

になります。 このことを使って円周率を計算するチャレンジャーが大勢現れました。

挑戦者達

Abraham Sharp (1651-1742)

$$\frac{\pi}{6}=\arctan\frac{1}{\sqrt{3}}.$$

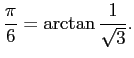
John Machin (1680-1752, ロンドン大学天文学教授) は 1706 年に

$$\frac{\pi}{4}=4\arctan\frac{1}{5}-\arctan\frac{1}{239}$$

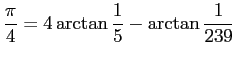
を用いて 100 桁の値を計算した。 以後この公式は多くの人達に採用されることになる。 William Shanks (1812-1882) が 707 桁計算したのが有名 (567 桁までが正しかった)。

L. Euler (1707-1783, スイスの Basel に生まれ、 ロシアの Petersburg に没する) は 1737 年に以下の公式を得た。

$$\frac{\pi}{4}=\arctan\frac{1}{2}+\arctan\frac{1}{3}, \quad \pi=20\arctan\frac{1}{7}+8\arctan\frac{3}{79}.$$

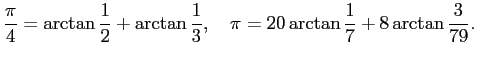
Charles Huttion (1737-1823) は 1776 年に次の結果を得た。

$$\frac{\pi}{4} =2\arctan\frac{1}{3}+\arctan\frac{1}{7} =2\arctan\frac{1}{2}-\arctan\frac{1}{7} =\arctan\frac{1}{2}+\arctan\frac{1}{3}$$

$$=3\arctan\frac{1}{4}+\arctan\frac{5}{99}.$$

有名な C. F. Gauss (Johann Carl Friedrich Gauss, 1777-1855) は、

$$\frac{\pi}{4}=12\arctan\frac{1}{18}+8\arctan\frac{1}{57} -5\arctan\frac{1}{239},$$

$$\frac{\pi}{4}=12\arctan\frac{1}{38}+20\arctan\frac{1}{57} +7\arctan\frac{1}{239}+24\arctan\frac{1}{268}$$

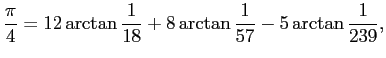
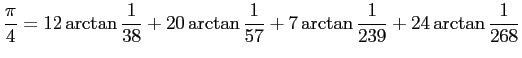
を発見した (1863年)。また 9 項からなる公式

$$\frac{\pi}{4} =2805\arctan\frac{1}{5257} -398\arctan\frac{1}{9466} +1950\arctan\frac{1}{12943} +1850\arctan\frac{1}{34208}$$

$$+2021\arctan\frac{1}{44179} +2097\arctan\frac{1}{85353} +1484\arctan\frac{1}{114669} +1389\arctan\frac{1}{330182}$$

$$+808\arctan\frac{1}{485298}$$

も得ていたとか (ちょっと唖然としますね -- もっとも並列計算でもしないと速くなりませんが)。

1896年にF. C. M. Störmer が得た次の公式は、 金田・うしろ後の世界記録 (2002) の検証計算にも使われたもので、 高い効率を実現します⁸。

$$\frac{\pi}{4}=44\arctan\frac{1}{57}+7\arctan\frac{1}{239}-12 \arctan\frac{1}{682}+24\arctan\frac{1}{12943}.$$

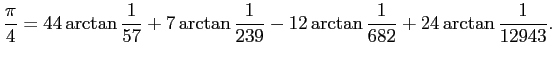
この解説を最初に書いた 2007年時点での円周率計算の世界記録は、 金田 康正, うしろ後 やすのり保範等の グループによるものでした (2013年現在の時点でどうなっているかは後述)。 これは 2002年に 1 兆 2400 億桁計算したというものですが、 そこでは、高野喜久雄⁹氏による公式 (1982)

$$\frac{\pi}{4} = 12\arctan\frac{1}{49}+ 32\arctan\frac{1}{57} - 5\arctan\frac{1}{239}+12\arctan\frac{1}{110443}$$

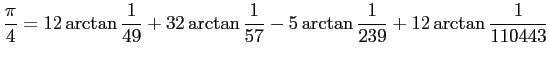
を用いたそうです (共立出版の雑誌 bit 1983年4月号への寄稿に、 この公式発見のいきさつが書いてあります)。