(準備中 -- この項は書きかけです。)
1976 年、![]() の計算法の歴史の新しい1ページが開かれました。
の計算法の歴史の新しい1ページが開かれました。
E. Salamin と R. P. Brent により独立に、次の手順が「発掘」されたのです。
| Salamin-Brent のアルゴリズム (別名 Gauss-Legendre のアルゴリズム) |
|
で定義された数列を用いて
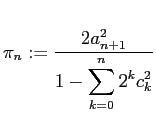
とおくとき、
|
これは無限級数でなく、
漸化式で定義された数列の極限として ![]() を
とらえているわけですが、いわゆる
を
とらえているわけですが、いわゆる ![]() 次の収束
(4) をするので非常に速く高精度の値が得られます。
収束の速さに関しては
次の収束
(4) をするので非常に速く高精度の値が得られます。
収束の速さに関しては