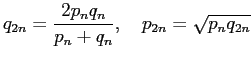

Next: 3 研究課題2
Up: 情報処理2 第5回 十進BASIC (2)
Previous: 1.5 レポート課題5B
これはレポートを提出するかどうか任意(余裕がある人向けの「挑戦課題」)。
締め切りはこの講義の最終回まで。
提出方法は、
syori2@math.meiji.ac.jp (@はASCIIの@) に電子メールを送ること。
半径 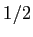 の円の円周 (の長さ) は、円周率
の円の円周 (の長さ) は、円周率 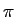 に等しい
(
に等しい
(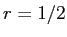 なので
なので
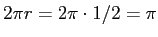 )。
有名なシラクサのアルキメデス (BC287?〜BC212) は、
内接正
)。
有名なシラクサのアルキメデス (BC287?〜BC212) は、
内接正 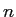 角形の周の長さ
角形の周の長さ 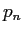 と、
外接正
と、
外接正 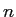 角形の周の長さ
角形の周の長さ 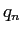 を考え、
を考え、
をもとにして、
実際に
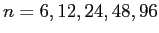 に対して
に対して 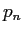 ,
, 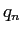 を計算して
(正六角形から始めて、辺の数を倍にしていった)、
を計算して
(正六角形から始めて、辺の数を倍にしていった)、
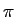 の評価を得た (「円の測定」という短い論文の中で、
の評価を得た (「円の測定」という短い論文の中で、
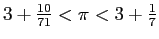 を証明している)。
アルキメデスは
を証明している)。
アルキメデスは 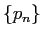 ,
, 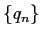 について成り立つ漸化式 (?)
について成り立つ漸化式 (?)
を用いて計算したという5。
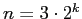 の場合、
すなわち内接・外接正
の場合、
すなわち内接・外接正
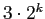 角形の周長をそれぞれ
角形の周長をそれぞれ 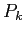 ,
, 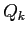 とおく:
とおく:
このとき 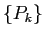 ,
, 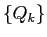 について成り立つ漸化式を導き、
について成り立つ漸化式を導き、
と合わせて用いて 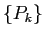 ,
, 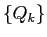 を計算するプログラムを作成し、
以下の (1), (2) に答えよ。
を計算するプログラムを作成し、
以下の (1), (2) に答えよ。
- (1)
- 正96角形 (
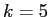 の場合) を利用すると、
の場合) を利用すると、
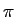 のどのような評価が得られるか。
のどのような評価が得られるか。
- (2)
- ネットで検索すると、
内接正多角形の周長で円周率の近似値を求めた歴史上の話が色々見つかる
(円周率マニアは多く、歴史のうんちく蘊蓄を語ってくれます)。
それらの話をいくつか選んで確認せよ
(正
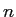 角形の周の長さを用いて小数点以下○○桁の値を求めたとある場合、
本当にそれができるか -- ときどきウソが書いてある)。
角形の周の長さを用いて小数点以下○○桁の値を求めたとある場合、
本当にそれができるか -- ときどきウソが書いてある)。
- (3)
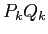 の
の 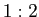 または
または 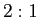 の比の内分点は、
の比の内分点は、
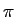 のより高精度な近似値となる。そのことを確めよ。
(どうしてそうなるか説明できたら素晴らしい。)
のより高精度な近似値となる。そのことを確めよ。
(どうしてそうなるか説明できたら素晴らしい。)
以下はヒント。
- もし高精度計算が必要な場合は、
OPTION ARITHMETIC DECIMAL_HIGH と宣言して、
1000桁演算を行うとよい。
- 十進BASICには、円周率の近似値を持つ
PI という定数が事前に定義されているので、
チェックに利用できる。


Next: 3 研究課題2
Up: 情報処理2 第5回 十進BASIC (2)
Previous: 1.5 レポート課題5B
桂田 祐史
2013-05-22
![]() の円の円周 (の長さ) は、円周率
の円の円周 (の長さ) は、円周率 ![]() に等しい
(
に等しい
(![]() なので
なので
![]() )。
有名なシラクサのアルキメデス (BC287?〜BC212) は、
内接正
)。
有名なシラクサのアルキメデス (BC287?〜BC212) は、
内接正 ![]() 角形の周の長さ
角形の周の長さ ![]() と、
外接正
と、
外接正 ![]() 角形の周の長さ
角形の周の長さ ![]() を考え、
を考え、