1.5 レポート課題5B

自然数 $n$ が与えられたときに

$$s_n:=\dsp\sum_{j=1}^n \dfrac{1}{j}, \quad t_n:=\dsp\sum_{j=1}^n \dfrac{1}{j^2},\quad r_n:=\dsp\sum_{j=1}^n \dfrac{1}{j^2+j}$$

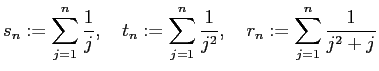
を計算するプログラムを書き、 $n=1$ , $10$ , $100$ , $1000$ , $\dots$ のとき⁴、値がどうなるか調べて (記録を取ること -- 紙に書いても良いですが、 COPY & PASTE してコンピューター上に残すのが間違いが起きづらいでしょう)、 $\{s_n\}$ , $\{t_n\}$ , $\{r_n\}$ が収束するか、発散するか、 予想して下さい。

なお、 $n\to\infty$ のときの極限については、 実は (数値計算しなくても) ある程度分かるはずです (収束・発散の区別については基礎数学4までの知識で判断出来るはず)。 なるべく、そのことを踏まえて結果を説明して下さい (確かに収束しそうだとか、発散しそうだとか、 もし極限値が分かっているならば第$n$ 項と極限値との差を計算してみる等)。

もっとも、この講義は、解析学ではないので、 極限が分からなければ、分からないでも構いません。 必要なのは、計算結果をきちんと示すことと、 その結果から数列が収束するのか、発散するのか、 収束する場合の極限値の見通しをつけることです。

レポートは TEX を使って kadai5b.pdf という名前の PDF ファイル を作成し、Oh-o! Meiji のレポート提出システムで送って下さい。 締め切りは、6月4日 (火曜) 18:00 とします。

TEX 文書は以下のような感じになるでしょう

kadai5b.tex

\documentclass[12pt]{jarticle}
\usepackage[a4paper]{geometry}% 好みの問題
\usepackage{amsmath,amssymb}% 今回は不要かも
\usepackage{moreverb}% 今回これが必要
\begin{document}
\title{情報処理2 課題5Bレポート}
\author{2年16組99番 数学 学}
\date{2013年5月15日}
\maketitle

\section{プログラム}

次のプログラムで $n=1,10,100,1000,10000$ のときの $s_n$, $t_n$, $r_n$ の値が
計算できます。

\listinginput{1}{kadai5b.BAS}% これで kadai5b.BAS を取り込みます。
                             % 複数あれば、同じように取り込めば良いでしょう。
\section{プログラムの実行結果}

kadai5b.BAS の実行結果は次のようになる。

\verbatimtabinput{kadai5b.TXT}% kadai5b.TXT を取り込みます。
% 必要ならば複数の実行結果を取り込めば良い。
% コピー＆ペーストで結果をまとめても構いません。
% その場合は verbatim 環境を使うのが簡単でしょうか。

\section{結果の分析}
(以下略)

\end{document}

工夫のヒント: 工夫すると、 1つのプログラムで複数の $n$ の値に対する $s_n$ , $t_n$ , $r_n$ の値を 一気に計算することができます。 もし無理なくできるならば、そういうプログラムを作ってみて下さい (加点要素になります)。