- ...
です1
- これを発見したのは Gauss です。
彼は定木とコンパスで正
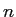 角形が作図出来るための条件を調べていて、
角形が作図出来るための条件を調べていて、
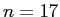 の場合にそれが可能であることを証明し、
実際に
の場合にそれが可能であることを証明し、
実際に
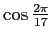 ,
,
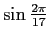 を
を
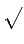 で表してみせました。
で表してみせました。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
となり2
- ここで、
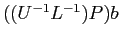 という順番にかけないのがミソである。
という順番にかけないのがミソである。
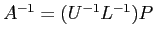 を計算するのは計算の手間がかかる。
特に
を計算するのは計算の手間がかかる。
特に 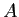 が疎行列の場合は、桁違いの差になるのが普通である。
が疎行列の場合は、桁違いの差になるのが普通である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...サブルーチン3
- 機械語 (machine language) や、
Fortran 言語における、あるまとまった処理をするプログラムの単位を
呼ぶ言葉。C 言語における「関数」に相当すると考えて構わない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... プログラミング言語4
- 当時は「自動プログラミング言語」
と呼ばれたそうである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...FORTRAN5
- FORTRAN は、
IBM が線形計画法のプログラムを効率的に作成するために開発した言語であると
言われている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...TNT6
- C++ 向けには
LAPACK++ があったが、C++ 言語の ANSI 規格の進展に伴い、
新しく設計し直されたのが TNT である。まだ発展途上で、LAPACK の機能のすべ
ては実装されていない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
公開されているフリーソフトである7
- このあたりに欧米文化の強さが
感じられる。ここで紹介したソフトの
中には、博士号クラスの研究者が数十人、何年も作業して始めて開発できたもの
もある。日本でも大学を中心に様々なライブラリィの開発がされたが、全面公開
までこぎつけたものは少なく (途中で企業に売ってしまったものもある)、大変
もったいない事態になっていると筆者は感じている。こうなってしまった背景に
は、ソフトウェアの開発を研究業績とは認めない風潮など、
二三の理由が考えられる…(脱線)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... インタープリター型言語である。そのため8
- ここで指摘することは、
例えば Mathematica, Maple, REDUCE のような数式処理系にも当てはま
る。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 注意深く利用しないと実行効率が低くなる9
- ここで述べたような注意
は、かつてはパソコン上で BASIC 言語を使ってプログラムを開発する際の常識
であったのだが、今ではあまり知られていないことなのだろう。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
命令が簡潔になっていて、プログラミングも楽になった10
- オブジェクト指向であり、
データ構造が隠蔽されていると言って良いかもしれない。
LAPACK などの利用で面倒な点の一つに、
プログラマーにライブラリィ中で定義されたデータ構造を正しくなぞったプログラムを
書く努力が要求されるというものがあるが、
MATLAB ではこれがなくなっている。
この点は C++ で書かれたライブラリィでも期待できることであるが。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... を学ぶことになっている11
- 実は「線形 (型) 代数」という
名前はそれほど古くからあるものではない。
かつては、「代数と幾何」、「行列と行列式」、
「線形数学」というような名前の本があったが (ちなみに、
筆者が学生の時の講義名は「代数と幾何」だった)、
現在では「線形 (型) 代数」に収束したようである。
個人的には収束と同時に「幾何」の匂いが薄れてきたように感じている
(みんな「代数」だと信じるようになったのかな -- 例えば
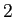 次,
次,
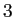 次の行列式が、それぞれ平行四辺形の符号付き面積、
平行六面体の符号付き体積を表わす (もちろん、これらはさらに一般の
次元に拡張される) ということを書いていない本が存在するが、
証明しなくても事実は教えておいた方が良いのにと思う)。
解析屋としては、
計量 (内積やノルム) の話があまり出て来ないことが残念である。
次の行列式が、それぞれ平行四辺形の符号付き面積、
平行六面体の符号付き体積を表わす (もちろん、これらはさらに一般の
次元に拡張される) ということを書いていない本が存在するが、
証明しなくても事実は教えておいた方が良いのにと思う)。
解析屋としては、
計量 (内積やノルム) の話があまり出て来ないことが残念である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
有限次元の線型空間とその間の線型写像の理論であるが12
- ちなみに、
解析的にこのテーマを取り扱った ``Finite dimensional vector spaces'' と
いうタイトルの有名な面白い本がある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 固有値問題13
- 応用上は、
一般化固有値問題という、行列
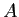 ,
, 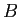 が与えられたときに、
が与えられたときに、
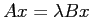 ,
, 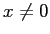 を満たす
を満たす 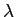 ,
, 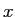 を求める問題も
重要 (分野によっては、標準固有値問題なんて目にしないことも) である。
を求める問題も
重要 (分野によっては、標準固有値問題なんて目にしないことも) である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 「掃き出し法」14
- 数値線形代数では、
ヨルダンJordan の消去法と呼ぶ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
された後は連立1次方程式を解くことに帰着されることが多い15
- 2001 年に書かれた文章によると、
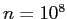 (1億) の問題が解かれているとか。
(1億) の問題が解かれているとか。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... に分類される16
- 今のところ、対称な問題に対しては、
CG 法の系統の解法がほとんど決定版とみなされている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 行列の疎性17
- 行列の成分に 0
が多いとき、
行列は疎 (sparse) であるという。
微分方程式の離散化で現われる連立1次方程式の係数行列は、
ほぼ例外無く疎行列である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 分解と呼ぶ18
- この分解について言及してある
線形代数の教科書は結構ある。Schmidt 分解とか Gram-Schmidt 分解と呼ばれる
ことが多いが、数値線形代数の世界ではもっぱら QR 分解と呼ばれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
適用することはない19
- 修正 Gram-Schmidt 法や、
基本的な直交変換 (例えば超平面に関する対称移動を表わす Householder 行列や、
二次元平面の回転を表わす Givens 行列) を次々にかけていく方法が使われる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.