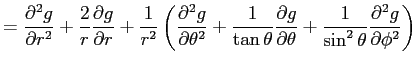

Next: この文書について...
Up: 情報処理2 第10回 Mathematica 体験
Previous: 2 レポート課題9 について
3 レポート課題10
締切は7月20日 (金) 18:00 とする
(というわけで解説はしません)。
Oh-o! Meiji で提出して下さい。
次のいずれかを選択して下さい。
なるべく (1) をしてもらいたいです。
- (1)
- 授業 (微積でなくても良く、数学でなくてもよい) などで現れた問題や例を、
Mathematica を使って計算してみる。
教科書、授業のノート、プリント、
自分が読んだ本 (授業と全然関係無くても良い) などから、
自分でやるのは大変そうな計算や、グラフ描画など、
適当な問題を探して、それを解く。
結果が正しいかどうか、検算したり、考えること。
- (2)
- Mathemaitca が計算できない、
あるいは間違えた結果を答えるような問題を見つけたら、
その理由を分析して、どの辺に限界があるか確めてみる。
- (3)
- 3次元空間のラプラシアン
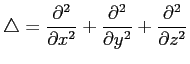 の極座標表示を
Mathematica を使って計算せよ。
の極座標表示を
Mathematica を使って計算せよ。
3次元極座標は色々な流儀がありますが、
ここでは「多変数の微分積分学1」で紹介した
を使って下さい。
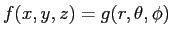 とすると、
とすると、
となるはずです。
手計算でやるとどうなるか、
http://nalab.mind.meiji.ac.jp/~mk/labo/text/polar-laplace.pdf にあります。
2次元のラプラシアンの極座標表示、半分手で、
半分コンピューターに解かせたものを
http://nalab.mind.meiji.ac.jp/~mk/labo/text/heat-fdm-2.pdfの付録 B.2 (p.105 付近) に書いてあります。


Next: この文書について...
Up: 情報処理2 第10回 Mathematica 体験
Previous: 2 レポート課題9 について
桂田 祐史
2012-09-02
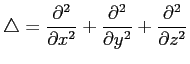 の極座標表示を
Mathematica を使って計算せよ。
の極座標表示を
Mathematica を使って計算せよ。
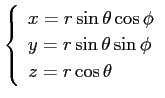
![$\displaystyle =\frac{\rd^2 g}{\rd r^2} +\frac{2}{r}\frac{\rd g}{\rd r} +\frac{1...
...d g}{\rd \theta}\right)+\frac{1}{\sin^2\theta}\frac{\rd^2 g}{\rd\phi^2} \right]$](img38.png)