1 レポート課題8 解説

「レポート課8」

うっかりしていました。締切りは先週だったから、 先週のうちに説明すれば良かったですね。

後で使いそうなものは変数に代入しておくのがコツの一つです。

(1)

「$661775625$ を素因数分解せよ。」
これは FactorInteger[ ] 一発ですね。

In[1]:= n=661775625
In[2]:= FactorInteger[n]

これで {{3, 2}, {5, 4}, {7, 6}} という結果を得ます。 $3^2 5^4 7^6$ という意味であるから、 素因数分解は $661775625=3^2\cdot 5^4\cdot 7^6$ . 確認するには

In[3]:= 3^2 5^4 7^6

あるいは 3^2 5^4 7^6-n として結果が 0 になることを確認する。

(2)

「$2^{15}-1$ と $2^{20}-1$ の最大公約数を求めよ。」
これも GCD[ ] 一発ですね。

In[4]:= a=2^15-1
In[5]:= b=2^20-1
In[6]:= GCD[a,b]

$31$ という結果を得ます。 やや強引 (能率の悪い手段) ですが、素因数分解してみます。

In[7]:= FactorInteger[a]
In[8]:= FactorInteger[b]

これから $2^{15}-1=7\cdot 31\cdot 151$ , $2^{20}-1=3\cdot 5^2\cdot 11\cdot 31\cdot 41$ が分かるので、目で見て $31$ が最大公約数であることが 分かります。 最大公約数は、 例えば Euclid の互除法などで効率的に計算出来ますが、 素因数分解は (わかりやすいけれど)、大きな桁数の整数の場合、 かなりの計算時間がかかってしまうことがまれではありません。
とっさに作ったので間違っているかも知れないけれど、 自分で互除法をする関数を作ってみて確認する例:

In[9]:= mygcd[m_,n_]:=If[n == 0, m, mygcd[n, Mod[m,n]]]
In[10]:= mygcd[a,b]

(3)

「$(a+b)^5$ の展開公式を作れ。」
これは楽勝ですね。 おっと、a と b の掃除を忘れずに (実は最初忘れてしまいました…)。

In[11]:= Clear[a,b,n]
In[12]:= Expand[(a+b)^5]
In[13]:= TeXForm[%]

a^5+5 a^4 b+10 a^3 b^2+10 a^2 b^3+5 a b^4+b^5 という結果を得ます。 これは TEX に取り込むのは簡単です。

$$\left(a+b\right)^5=a^5+5 a^4 b+10 a^3 b^2+10 a^2 b^3+5 a b^4+b^5.$$

(4)

「$2$ 次方程式 $x^2+a x+b=0$ を解け。 $3$ 次方程式 $x^3+p x+q=0$ を解け。 」
これは $ax$ を a*x や a x と間違えずに入力すれば問題な いでしょう。

In[14]:= sol=Solve[x^2+a x+b==0,x]

結果を取り込むのにちょっと工夫。

In[15]:= {x1,x2} = x/. sol
In[16]:= TeXForm[x1]
In[17]:= TeXForm[x2]

これから

$$x=\frac{1}{2} \left(-\sqrt{a^2-4 b}-a\right), \frac{1}{2} \left(\sqrt{a^2-4 b}-a\right).$$

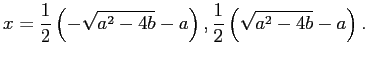
もちろん授業でやったように、結果を $x^2+a x+b$ に代入して確かめる、 という手もあります。

In[18]:= x^2+a x+b /. sol
In[19]:= Simplify[%]

結果は {0, 0} になりました。

一方 $x^3+p x+q=0$ の方も同様にやると

$$x =\frac{\sqrt[3]{\sqrt{3} \sqrt{4 p^3+27 q^2}-9 q}}{\sqrt[3]{2} 3^{2/3}}-\frac{\sqrt[3]{\frac{2}{3}} p}{\sqrt[3]{\sqrt{3} \sqrt{4 p^3+27 q^2}-9 q}},$$

$$\frac{\left(1+i \sqrt{3}\right) p}{2^{2/3} \sqrt[3]{3} \sqrt[3]{\... ...t{3}\right) \sqrt[3]{\sqrt{3} \sqrt{4 p^3+27 q^2}-9 q}}{2 \sqrt[3]{2} 3^{2/3}},$$

$$\frac{\left(1-i \sqrt{3}\right) p}{2^{2/3} \sqrt[3]{3} \sqrt[3]{\... ...t{3}\right) \sqrt[3]{\sqrt{3} \sqrt{4 p^3+27 q^2}-9 q}}{2 \sqrt[3]{2} 3^{2/3}}.$$

ごちゃごちゃしていて、訳がわかりませんね。 式の簡単化はまだコンピューターまかせは難しいです (しかし上と同様に $x^3+p x+q$ に代入して、 Simplify[ ] すると、ちゃんと 0 になります)。

(5)

「次の関数を微分せよ。 (i) $x^2\sqrt{x}+(x^3-x)\sqrt{x^2+x+1}$ (ii) $$\sqrt{\frac{1+x^2}{1-x^2}}$$ 」
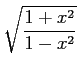するだけならば簡単。

In[18]:= y=D[x^2 Sqrt[x] + (x^3 - x) Sqrt[x^2 + x + 1], x]
In[19]:= Simplify[y]

Simplify[ ] するのが良いかどうか、分かりにくいですね。 両方書いておきます。

$$\left(x^2\sqrt{x}+(x^3-x)\sqrt{x^2+x+1}\right)' =\frac{5 x^{3/2}}{2}+\sqrt{x^2+x+1} \left(3 x^2-1\right)+\frac{(2 x+1) \left(x^3-x\right)}{2 \sqrt{x^2+x+1}}$$

$$=\frac{8 x^4+7 x^3+2 x^2+5 \sqrt{x^2+x+1} x^{3/2}-3 x-2}{2 \sqrt{x^2+x+1}}.$$

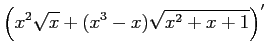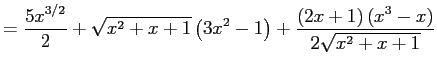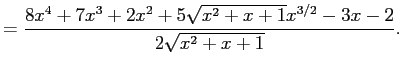これは確認計算が難しいですね。 バカバカしいですが、積分してみることは出来ます (普通は難しい積分の確認をするのに微分してみるものですが…)。

In[20]:= Integrate[y,x]

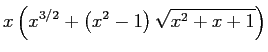結果は $\dsp x\left(x^{3/2}+\left(x^2-1\right) \sqrt{x^2+x+1}\right)$ と元に戻りました。 一方、

In[20]:= y=D[Sqrt[(1+x^2)/(1-x^2)],x]
In[21]:= Simplify[y]

これから

$$\left(\sqrt{\frac{1+x^2}{1-x^2}}\right)'= \frac{2 x}{\left(x^2-1\right)^2 \sqrt{\frac{x^2+1}{1-x^2}}}.$$

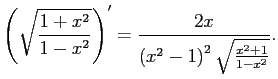
これも Integrate[y,x] で元に戻るのが確認出来ます。

(6)

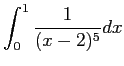「(i) $$\int_0^1\frac{1}{(x-2)^5} \D x$$ (ii) $$\int_0^\pi\frac{1}{2+\cos x} \D x$$ 」

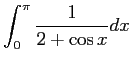In[22]:= Integrate[1/(x-2)^5,{x,0,1}]
In[23]:= Integrate[1/(2+Cos[x]),{x,0,Pi}]

$$\int_0^1\frac{1}{(x-2)^5} d x=-\frac{15}{64},\quad \int_0^\pi\frac{1}{2+\cos x} dx=\frac{\pi}{\sqrt{3}}.$$

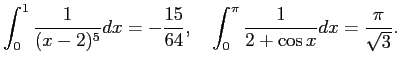
検算はやはり不定積分を微分して元の関数に戻ること、 その不定積分を元に定積分の計算をしてみるくらいでしょうか。

In[24]:= y=Integrate[1/(x-2)^5,x]
In[25]:= D[y,x]
In[26]:= (y /. x->1) - (y /. x->0)

Out[25] で元の関数が出て来て、 Out[26] は $-\dfrac{15}{64}$ となります。