

Next: 4 レポート課題X予告
Up: 情報処理2 第8回 Mathematica 体験
Previous: 2.3 数式処理とは
(今日 (6月6日) は、
『Mathematica入門』
の 4, 5 節を説明する予定です。
このレポート課題 8 を解くために必要なことは、
そこに説明されています。
『Mathematica入門』では色々な計算をさせていますが、
なぜそういう結果になるか考えて
(場合によっては計算前に結果を予想して)、
なるべくそれを自分の目の前のコンピューターで再現して下さい。)
以下の問題 (1)〜 (6) を Mathematica を用いて解いて、
レポートせよ。
- 提出先は、
SNSトピック「第8回(2012/6/6)」
です。
締め切りは6月19日 (火曜), 18:00 です。
- 実際の計算の様子が分かるように、
ノートブックを [ファイル] 欄に添付すること。
ノートブックの名前は、``kadai8.nb'' にすること。
- ノートブックの保存については、
「レポート提出用のノートブックを作る」
を参考にして下さい。
今の Mathematica は「LaTeXドキュメント」で保存する機能があるので、
LATEX で計算結果も含めた PDF ドキュメント kadai8.pdf
を作成することも可能である。
余裕があればそれにチャレンジしてみること (ボーナス点を与える)。
- 計算問題の答を可能な限り本文に書くこと
(なるべく A 「数学SNSで TEX 画像を使う」 を見て、
TEX 画像の利用に挑戦して下さい -- TEX 画像使えれば
(4) の後半以外は楽勝のはず,
(4) の後半は「kadai8.nbを参照して下さい」で構いません)。
- 計算結果が複雑な場合は、簡単化 (例えば Simplify[]) を試みること。
- 変数に以前計算した値が残っていて、
期待する結果が得られないことが時々あります。
Clear[] や Remove[] を用いて、
古い記憶を消去すると良いでしょう (Clear[a,b] のように使います)。
- 検算が可能な問題については、検算もすること。
-- 時間に余裕が生じた場合は、ここを頑張ること。
- (1)
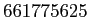 を素因数分解せよ。
を素因数分解せよ。
- (2)
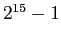 と
と 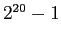 の最大公約数を求めよ。
の最大公約数を求めよ。
- (3)
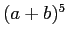 の展開公式を作れ。
の展開公式を作れ。
- (4)
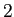 次方程式
次方程式
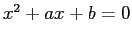 を解け。
を解け。
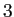 次方程式
次方程式
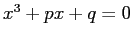 を解け。
を解け。
- (5)
- 次の関数を微分せよ。
(i)
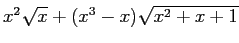 (ii)
(ii)
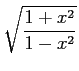
- (6)
- (i)
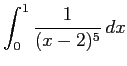 (ii)
(ii)
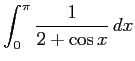
(余談) (4) で3次方程式を
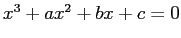 と
していないのは、結果が複雑過ぎるからです
(一度試してみましょう)。
簡単な変数変換 (カルダノ変換という) で、
2次の係数が 0
の方程式
と
していないのは、結果が複雑過ぎるからです
(一度試してみましょう)。
簡単な変数変換 (カルダノ変換という) で、
2次の係数が 0
の方程式
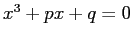 に変換されるので、
それを解ければ良いことになります。
に変換されるので、
それを解ければ良いことになります。
よくある間違い
例えば 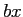 は、bx でなく (これでは一つの名前になってしまう)、
掛け算演算子 * を使って b*x、
あるいはブランクを入れて b x とする。
は、bx でなく (これでは一つの名前になってしまう)、
掛け算演算子 * を使って b*x、
あるいはブランクを入れて b x とする。


Next: 4 レポート課題X予告
Up: 情報処理2 第8回 Mathematica 体験
Previous: 2.3 数式処理とは
桂田 祐史
2012-06-06
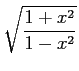
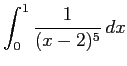 (ii)
(ii)
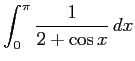
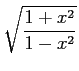
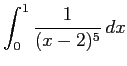 (ii)
(ii)
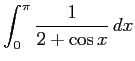
![]() と
していないのは、結果が複雑過ぎるからです
(一度試してみましょう)。
簡単な変数変換 (カルダノ変換という) で、
2次の係数が 0
の方程式
と
していないのは、結果が複雑過ぎるからです
(一度試してみましょう)。
簡単な変数変換 (カルダノ変換という) で、
2次の係数が 0
の方程式
![]() に変換されるので、
それを解ければ良いことになります。
に変換されるので、
それを解ければ良いことになります。
![]() は、bx でなく (これでは一つの名前になってしまう)、
掛け算演算子 * を使って b*x、
あるいはブランクを入れて b x とする。
は、bx でなく (これでは一つの名前になってしまう)、
掛け算演算子 * を使って b*x、
あるいはブランクを入れて b x とする。