6.3 Descartes の正葉線

Descartes の正葉線 (デカルトの葉形, folium of Descartes, 1638年)

$$x^3+y^3-3axy=0$$

$y=tx$ とおくと、有理パラメーター表示

$$x=\frac{3at}{1+t^3},\quad y=\frac{3at^2}{1+t^3}$$

を得る。

$x=r\cos\theta$ , $y=r\sin\theta$ を代入すると、極形式の表示

$$r=\frac{3a\sin\theta\cos\theta}{\sin^3\theta+\cos^3\theta}$$

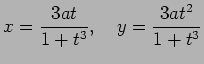
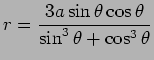
を得る。

gnuplot で

  a=1
  f(x,y)=x**3+y**3-3*a*x*y
  set xrange [-3*a:3*a]
  set yrange [-3*a:3*a]
  set view 0,0
  set isosample 100,100
  set size square
  set cont base
  set cntrparam level incre 0,0.1,0
  unset surface
  set nokey
  #set border 0
  #set noxtics
  #set noytics
  set xzeroaxis lt 0
  set yzeroaxis lt 0
  splot f(x,y)

図 7: gnuplot

Mathematica で

 Needs["Graphics`ImplicitPlot`"]
 g = ImplicitPlot[x^3 + y^3 - 3 x y == 0, {x, -2.5, 2}]

図 8: Mathematica