


Next: A.8.0.0.2 �$BDc
Up: A.8 �$B
Previous: A.8 �$B
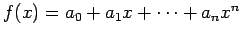 �$B$r0x;R�(B
�$B$r0x;R�(B 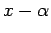 �$B$K$h$C$F�(B
�$B9b
�$B$K$h$C$F�(B
�$B9b
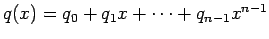 �$B$r�(B
�$B5a$a$k!#�(B
�$B$r�(B
�$B5a$a$k!#�(B
-
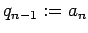 �$B$H$*$/!#�(B
�$B$H$*$/!#�(B
-
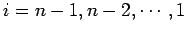 �$B$N=g$K!"0J2<$r7+$jJV$9!#�(B
�$B$N=g$K!"0J2<$r7+$jJV$9!#�(B
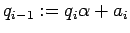 .
.
-
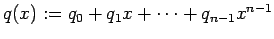 �$B$H$*$/!#�(B
�$B$H$*$/!#�(B



Next: A.8.0.0.2 �$BDc
Up: A.8 �$B
Previous: A.8 �$B
Masashi Katsurada
�$BJ?@.�(B21�$BG/�(B7�$B7n�(B9�$BF|�(B