C. Eigen ライブラリィを用いた Jordan 領域の等角写像の計算プログラム

本文中に Python を用いたサンプル・プログラムを載せた。以前は C++ を用いていた。参考までそれも載せておく。

個人的には、この手の計算には MATLAB を使うのが好みであるが、ここでは、C++ でベクトル、行列に関する演算をするために便利なクラス・ライブラリィである、 Eigen を利用してみる (なお、C++ では、複素数を使うのも簡単である)。

WWWサイトから、 eigen-eigen-5a0156e40feb.tar.gz のような名前のソース・ファイル一式を入手して、以下のようにインストールする。
MacBook のターミナルで次のようにインストール

tar xzf eigen-eigen-5a0156e40feb.tar.gz cd eigen-eigen-5a0156e40feb ls
(Eigen があることを確認)
cp -pr Eigen /include あるいは cp -pr Eigen /usr/local/include
アーカイブ・ファイルに含まれていた、Eigen というディレクトリィを、~/include や /usr/local/include の下にコピーしている。

(脱線になるけれど、Eigen を用いた、 Runge-Kutta 法のサンプル・プログラム http://nalab.mind.meiji.ac.jp/~mk/complex2/ball-bound.cppを紹介しておく。コンパイルの仕方、実行の仕方は、注釈に書いてある。)

$\Omega=D_1=D(0;1)$ , の場合を解いてみよう。つまり双正則な

$\displaystyle \varphi\colon \Omega\to D_1$

で、

$\displaystyle \varphi(z_0)=0,\quad \varphi'(z_0)>0$

を満たすものを求める。この場合は、1次分数変換

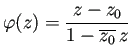
$\displaystyle \varphi(z)=\frac{z-z_0}{1-\overline{z_0} z}$

が解であることが分かっている。

conformalmap.cpp -- 例えばターミナルで

curl -O http://nalab.mind.meiji.ac.jp/~mk/complex2/conformalmap.cpp

としてダウンロード出来る。

/*
 * conformalmap.cpp --- 等角写像の数値計算例 (基本解の方法の天野要氏バージョン)
 *
 * g++ -I/opt/X11/include -I/usr/local/include conformalmap.cpp 
 *   -L/usr/local/lib -lglscd -L/opt/X11/lib -lX11
 *  これは /opt/X11 に X 関係のファイルが、
 *         /usr/local に Eigen, GLSC 関係のファイルが
 *  あると仮定している。
 *
 *   現象数理学科 Mac では、GLSC は ~/include, ~/lib にインストールして
 * あるだろうから、次のようにするのかな。
 * g++ -I/opt/X11/include -I ~/include conformalmap.cpp -L ~/lib -lglscd -L/opt/X11/lib -lX11
 * その場合は、Eigen も ~/include にインストールすると良い。
 * まあ、適宜やって下さい。
 */

#include <iostream>
#include <complex>
#include <Eigen/Dense>

extern "C" {
#include <glsc.h>
};

using namespace std;
using namespace Eigen;

// MatrixXd は大きさが実行時に指定できて、成分が double の行列
// d(double) の代わりに i(int), f(float), cf, cd (complex<double>) もOK

// φ(z0)=0, φ'(z0)>0 を満たす等角写像
complex<double> phi(complex<double> z,
		    complex<double> z0)
{
  complex<double> w;
  w = (z-z0)/(1.0-conj(z0)*z);
  return w;
}

// 天野の方法による等角写像
complex<double> f(complex<double> z,
		  complex<double> z0,
		  int N,
		  double Q0, 
		  VectorXd Q, VectorXcd zeta)
{
  int k;
  complex<double> s;
  s = Q0;
  for (k = 0; k < N; k++)
    s += Q(k) * log((z-zeta(k))/(z0-zeta(k)));
  return (z-z0) * exp(s);
}

int main(void)
{
  int i, j, k, N, m;
  double theta, pi, dt, R, Q0, r, dr;
  // 虚数単位と原点に移る点 z0=1/2
  complex<double> I(0,1), z0(0.6,0.0), zp, w, w2;

  R = 2;
  N = 80;
  VectorXcd zeta(N), z(N);
  VectorXd b(N), Q(N);
  MatrixXd a(N,N);

  pi = 4.0 * atan(1.0);
  dt = 2 * pi / N;
  // 円周 |z|=2 上の等分点
  for (k = 0; k < N; k++)
    zeta(k) = R * exp(I * (k * dt));
  //  cout << "zeta=" << zeta << endl;
  // 単位円周 |z|=1 上の等分点
  for (j = 0; j < N; j++)
    z(j) = exp(I * (j * dt));

  // 係数行列の準備
  for (j = 0; j < N; j++)
    for (k = 0; k < N; k++) {
      a(j,k) = log(abs(z(j)-zeta(k)));
    }
  // 右辺
  for (j = 0; j < N; j++) {
    b(j) = - log(abs(z(j)-z0));
  }
  // 電荷を求める
  Q = a.partialPivLu().solve(b);

  // Q0 を求める
  Q0 = 0;
  for (k = 0; k < N; k++) {
    Q0 += Q(k) * log(abs(z0-zeta(k)));
  }

  g_init((char *)"GRAPH", 150.0, 150.0);
  g_device(G_BOTH);
  g_def_scale(0, - 1.2, 1.2, -1.2, 1.2, 10.0, 10.0, 140.0, 140.0);
  g_sel_scale(0);

  m = 20;
  // 同心円の像
  dr = 1.0 / m;
  dt = 2 * pi / (4 * m);
  for (i = 1; i <= m; i++) {
    r = i * dr;
    for (j = 0; j <= 4 * m; j++) {
      zp = r * exp(I * (j * dt));
      w=f(zp,z0,N,Q0,Q,zeta);
      if (j == 0)
        g_move(w.real(), w.imag());
      else
        g_plot(w.real(), w.imag());
    }
  }
  // 放射線の像
  for (j = 0; j <= 4 * m; j++) {
    theta = j * dt;
    for (i = 0; i <= m; i++) {
      r = i * dr;
      zp = r * exp(I * theta);
      w=f(zp,z0,N,Q0,Q,zeta);
      if (i == 0)
        g_move(w.real(), w.imag());
      else
        g_plot(w.real(), w.imag());
    }
  }
  g_sleep(-1.0);
  g_term();
  return 0;
}

こんな風にコンパイル

g++ -I/opt/X11/include -I ~/include conformalmap.cpp -L ~/lib -lglscd -L/opt/X11/lib -lX11
(GLSC を利用していて、現象数理学科 Mac では、 ~/include, ~/lib にインストールされていることを想定している。上の手順で、 Eigen も ~/include にインストールしておいた。)

**図 10:** $w=\dfrac{z-z_0}{1-\overline{z_0} z}$ , による平面の同心円、放射線の像を描いた。

桂田祐史