簡単のため、同次 Dirichlet 境界条件 (
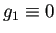 ) の場合に説明する。
) の場合に説明する。
とおくと、差分方程式から次のような連立1次方程式が得られる:
ここで 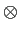 は行列のテンソル積を表す記号であり、
は行列のテンソル積を表す記号であり、
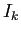 は
は 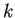 次の単位行列、
次の単位行列、
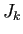 は次の形の
は次の形の 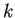 次正方行列であるとする。
次正方行列であるとする。
(詳しくは桂田 [5] を見よ。)
プログラムを書くときのために、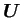 ,
, 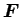 の成分
の成分
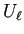 ,
, 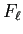 を式で表しておく。
を式で表しておく。
つまり、領域内部の格子点 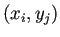 を1次元的に並べて番号をつけた
8、
ということである。
並べ方は一通りではなく、(B.18) の代わりに
を1次元的に並べて番号をつけた
8、
ということである。
並べ方は一通りではなく、(B.18) の代わりに
|
(B.19) |
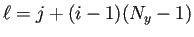 |
というものも良く使われる。
(B.18) を row first,
(B.19) を column first と呼んで区別する。
次に紹介する MATLAB プログラムでは、
(B.18) を採用してある。
桂田 祐史
![]() ) の場合に説明する。
) の場合に説明する。
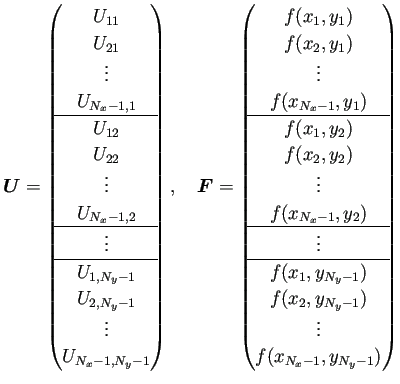
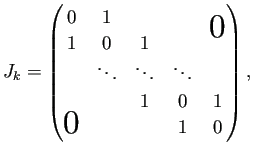
![]() ,
, ![]() の成分
の成分
![]() ,
, ![]() を式で表しておく。
を式で表しておく。