Next: 2.2.1 複合中点公式 Up: 2 補間型数値積分公式 Previous: 2.1.3 Rungeの現象があるので
区間 ![]() から標本点
から標本点
![]() を選び出したとき、
関数
を選び出したとき、
関数 ![]() の補間多項式
の補間多項式 ![]() が定まるが、
それは多項式であるから、
が定まるが、
それは多項式であるから、
| (9) |
| (再掲 (2)) | 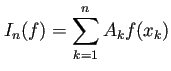 |
小さい ![]() に対して名前がついている。それを紹介しよう。
(授業では、図を板書すること。)
に対して名前がついている。それを紹介しよう。
(授業では、図を板書すること。)
| (10) | 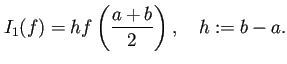 |
| (11) | 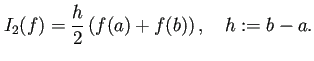 |
| (12) | 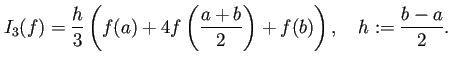 |
| (13) | 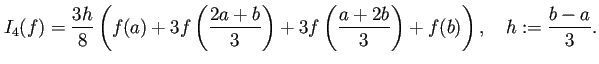 |
これらの公式の導出は、一般的に行うことも出来るが、
実際に使われるのは、
![]() までなので、気張らないことにして省略する (やれば出来る)。
までなので、気張らないことにして省略する (やれば出来る)。
![]() の場合はほとんんど使われない
(というか、実は
の場合はほとんんど使われない
(というか、実は ![]() の場合もあまり使われない)。
の場合もあまり使われない)。
数値積分公式が ![]() 位の公式 (
位の公式 (![]() 次の精度) であるとは、
関数
次の精度) であるとは、
関数 ![]() の数値積分公式の誤差を
の数値積分公式の誤差を ![]() と書くとき、
と書くとき、
| (14) |
補間型数値積分公式 ![]() は作り方から、少なくとも
は作り方から、少なくとも ![]() 位の公式であるが、
実は
位の公式であるが、
実は ![]() が奇数のとき、
が奇数のとき、![]() 位の公式である。
例えば、
中点公式
位の公式である。
例えば、
中点公式 ![]() と台形公式
と台形公式 ![]() はともに
はともに![]() 位の公式で、
Simpson公式
位の公式で、
Simpson公式 ![]() とSimpson
とSimpson
![]() 公式
公式 ![]() は
ともに
は
ともに![]() 位の公式である。
位の公式である。