Next: 2.1.2 Runge „ÅÆÁèæ˱° Up: 2.1 Ë£úÈñì§öÈÝÖºè Previous: 2.1 Ë£úÈñì§öÈÝÖºè
| (3) | 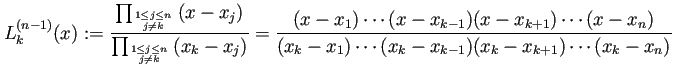 |
| (4) |
| (5) | 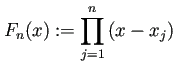 |
| (6) | 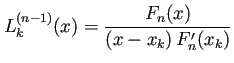 |
| (7) | 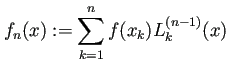 |
‰ª•‰∏ä„ÅßÂ≠òÂú®„ÅåÁ§∫„Åõ„Åü„ÄÇ![]() ʨ°Â§öÈÝÖºè„ÅƉøÇÊï∞
ʨ°Â§öÈÝÖºè„ÅƉøÇÊï∞
![]() (つまり
(つまり
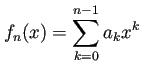 ということ)
„Çí
ということ)
„Çí ![]() ,
, ![]() ,
, ![]() ,
, ![]() での値
での値 ![]() ,
, ![]() ,
,
![]() ,
, ![]() を対応させる写像は、
を対応させる写像は、
![]() „Åã„Çâ
„Åã„Çâ
![]() への線型写像である。
上でそれが全射であることが分かった。
線形代数で学ぶ定理によって、それは単射である。
„Åì„Çå„ÅØ
への線型写像である。
上でそれが全射であることが分かった。
線形代数で学ぶ定理によって、それは単射である。
これは ![]() が一意的に定まることを意味している。
が一意的に定まることを意味している。 ![]()
![]()
![]() ,
, ![]() ,
,
![]() „Çí„ÄÅ
„Çí„ÄÅ
![]() ,
, ![]() ,
, ![]() を標本点とする Lagrange 補間係数と呼ぶ。
を標本点とする Lagrange 補間係数と呼ぶ。
上の定理の ![]() を
„Çí ![]() „ÅÆË£úÈñì§öÈÝÖºè (interpolating
polynomial) と呼ぶ。
上の議論から分かるように
„ÅÆË£úÈñì§öÈÝÖºè (interpolating
polynomial) と呼ぶ。
上の議論から分かるように
| (8) | 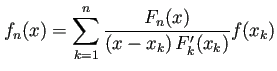 |
(Newton„ÅÆË£úÈñìÂ֨ºè (Newton Ë£úÈñì§öÈÝÖºè, Newton polynomial) „Å®„ÅÑ„ÅÜ„ÇÇ„ÅÆ„ÇÇ„ÅÇ„Çã„Åå„ÄŠˣúÈñì§öÈÝÖºè„Åß„ÅÇ„Çã„Åì„Å®„Å´„Åاâ„Çè„Çä„Åå„Å™„ÅÑ„ÄÇ)
桂田 祐史