Next: 5.4 誤差の特性関数の例 (2) 無限区間の台形公式 Up: 5 数値積分の高橋・森による誤差解析理論 Previous: 5.2 有理関数の積分への応用
![]() ,
, ![]() の場合の
の場合の ![]() 点複合シンプソン公式
点複合シンプソン公式 ![]()
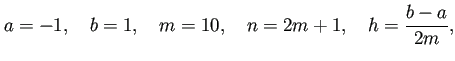
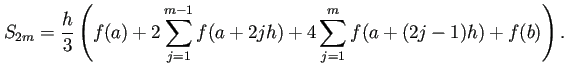
![$\displaystyle w_k=
\left\{
\begin{array}[tb]{ll}
h/3 & \text{($k=0,2m$)} \ ...
...ots,m-1$)} \\
4h/3 & \text{($k=2j-1$, $j=1,2,\dots,m$)}
\end{array} \right.
$](img254.png)
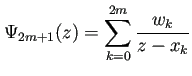
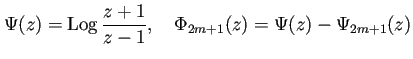
(これは森 [12] にある図と見比べるためである。)
![]() 平面において、積分区間
平面において、積分区間 ![]() から遠ざかると、
から遠ざかると、
![]() が急速に減少することが分かる。
このような挙動が多くの数値積分公式に共通して見られることは、
が急速に減少することが分かる。
このような挙動が多くの数値積分公式に共通して見られることは、
![[*]](crossref.png) で述べたことから理解できる。
で述べたことから理解できる。
この図は実際的な誤差評価に使うことが出来る。
もう1つ、有限区間上の数値積分公式の誤差の特性関数の例をあげておく。 この講義では解説していないが、 有名な Gauss-Legendre 公式の場合を紹介する。
![]() 次の Gauss-Legendre 公式は、
次の Gauss-Legendre 公式は、
![]() 次の直交多項式の
次の直交多項式の![]() 個の零点を標本点に使い、
個の零点を標本点に使い、
![]() 次までの多項式について正確な積分を計算できる。
つまり15位の公式である。
実際
次までの多項式について正確な積分を計算できる。
つまり15位の公式である。
実際
![]() の曲線が見え、
の曲線が見え、
![]() 点 Simpson 公式よりも格段に誤差の特性関数の値が小さい
(
点 Simpson 公式よりも格段に誤差の特性関数の値が小さい
(![]() 桁下、つまり1億分の1) ことが分かる。
桁下、つまり1億分の1) ことが分かる。
桂田 祐史