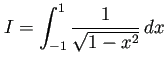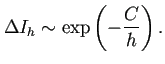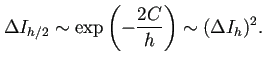- (名前の由来)
要するに変数変換後に得られる被積分関数
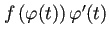 (
(
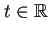 ) が二重指数関数的に減衰する:
) が二重指数関数的に減衰する:
- 端点における特異性に強い。例えば次のような積分でもうまく計算できる。
- (誤差の性質)
これから
これから (刻み幅が十分小さい場合)
刻み幅を半分にすると、結果の有効桁数が 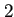 倍になる。
(
倍になる。
(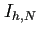 についても、
についても、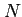 を十分大きくとって、
を十分大きくとって、
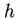 を半分、
を半分、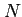 を
を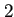 倍にすると、同様の挙動を示すと期待出来る。)
倍にすると、同様の挙動を示すと期待出来る。)
- Simpson 則などと比べて桁違いに高性能
- 同じ手間で精度が何桁も良い
- 同じ精度を得るのに手間が桁違いに少ない
- Gauss 型公式 (DE公式発見以前は究極の公式だった) と比べても
- やはり桁違いに高性能 (Simpson 則との比較と同様)
- 自動積分が出来るのは有利 (これが出来ないのは Gauss 型公式の弱点)
- 分点や重みが計算しやすい (Gauss 型の場合は手間がかかり注意が必要 -- 面倒)
- 低次の多項式に対しても誤差が 0 とはならない (固有誤差)。
- アンダーフロー、オーバーフローが起こりやすく、
プログラムを書くときに注意が必要である。
桂田 祐史