Next: 2.2.2 1次元の場合の有限要素法 Up: 2.2.1 1次元の場合の弱解の方法 Previous: 2.2.1 1次元の場合の弱解の方法
![$\displaystyle -\left[u'(x)v(x)\right]_0^1+\int_0^1 u'(x)v'(x)\;\Dx=
\int_0^1 f(x)v(x)\;\Dx.
$](img66.gif)
ゆえに
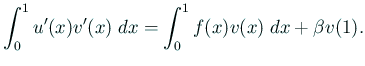
すなわち
![]()
次に変分問題3(variational problem) にしたものを述べる。
| 問題 (V) |
|
を満たすものを求めよ。ただし
![$\displaystyle J[u]:=\frac{1}{2}\int_0^1 \left\vert u'(x)\right\vert^2\Dx-
\int_0^1 f(x)v(x)\;\Dx-\beta v(1).
$](img74.gif)
|
![]() が汎関数であることに注意しよう。
が汎関数であることに注意しよう。
(W) と (V) は同値な問題であり、 常に一意的な解を持つことが比較的容易に分かる。

逆に ![]() がある程度滑らかであれば、
(W), (V) の解は (P) の解であることが示される。
がある程度滑らかであれば、
(W), (V) の解は (P) の解であることが示される。
問題 (V) の解 (それは (W) の解でもある) が![]() 級であることを認めると、
(P), (W), (V) は互いに同値な問題ということになる。
(W)
級であることを認めると、
(P), (W), (V) は互いに同値な問題ということになる。
(W) ![]() (P) は、Dirichlet 原理の一般化である
(Laplace 方程式のDirichlet境界値問題の場合、
この
(P) は、Dirichlet 原理の一般化である
(Laplace 方程式のDirichlet境界値問題の場合、
この ![]() は Dirichlet 積分 (の
は Dirichlet 積分 (の![]() 倍) に他ならない。)。
倍) に他ならない。)。
そこで問題 (P) を解く代わりに、(W) あるいは (V) を解くことを目指す。
通常、変分法は、変分問題を解くために、それと同値な微分方程式の問題を導き、 そちらを解くことで変分問題の解を得るのが普通であるが、 ここでは逆に微分方程式の問題を解くために、それを変分問題に書き換え、 それを直接解く、という手順の議論をしている。 これは、変分法の直接法と呼ばれるものになっている。
桂田 祐史