A..3.1 差分方程式

$N_x$ , $N_y\in\mathbb{N}$ に対して、

$$h_x=\Delta x:=\frac{W}{N_x},\quad h_y=\Delta y:=\frac{H}{N_x},$$

$$x_i=i\Delta x 0\le i\le N_x ,\quad y_j=j\Delta y 0\le j\le N_y$$

によって格子点 $(x_i,y_j)$ を定める。

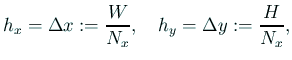領域内部にある格子点のインデックスの集合を

$$\omega:=\left\{(i,j)\relmiddle\vert 1\le i\le m, 1\le j\le n\right\}, \quad m:=N_x-1,\quad n:=N_y-1,$$

領域の境界上にある格子点のインデックスの集合を

$$\gamma:= \left\{(i,0)\relmiddle\vert\le i\le N_x\right\} \cup \... ...rt\le j\le N_y\right\} \cup \left\{(N_x,j)\relmiddle\vert\le j\le N_y\right\}$$

とおく。個数を調べておこう。

$$\sharp\omega=(N_x-1)(N_y-1)=mn,\quad \sharp\gamma=2(N_x+N_y),\quad \sharp(\omega\cup\gamma)=(N_x+1)(N_y+1).$$

$$-\frac{U_{i+1,j}-2U_{i,j}+U_{i-1,j}}{\Delta x^2} -\frac{U_{i,j+1}-2U_{i,j}+U_{i,j-1}}{\Delta y^2} =f(x_i,y_j) (i,j)\in\omega ,$$ (A.13)

$$U_{i,j}=g_1(x_i,y_j) (i,j)\in\gamma ,$$ (A.14)

という差分方程式の解 $U_{ij}$ を $u(x_i,y_j)$ の近似値とするのが良いと 期待できる。

これは $(N_x+1)(N_y+1)$ 個の未知数 $U_{i,j}$ ( $(i,j) \in\omega\cup\gamma$ ) についての、 $(N_x+1)(N_y+1)$ 個の1次方程式である。 $U_{i,j}$ ( $(i,j)\in\gamma$ ) は (A.14) から分かるので、 それを (A.13) に代入して消去すると、 $(N_x-1)(N_y-1)$ 個の未知数 $U_{i,j}$ ( $(i,j)\in\omega$ ) についての、

$$N:=(N_x-1)(N_y-1)$$ (A.15)

個の1次方程式が得られる。

未知数の個数と方程式の個数が等しいので、 正方行列を係数とする連立１次方程式の形に表せるはずである。 実際にそうするためには、$U_{i,j}$ を並べて1つのベクトルにする必要がある。

以下このことを実行するが、自分でプログラムを書く必要が生じるまで、 読む必要はないであろう。