Next: 5.3 近似等角写像を求めるための天野の方法 Up: 5 Laplace 方程式に対する基本解の方法 Previous: 5.1.3 Green の積分公式 (続き)
簡単のため、
![]() の場合の Laplace 方程式の境界値問題
の場合の Laplace 方程式の境界値問題
![]() が滑らかな境界を持つ有界領域の場合に、
この境界値問題が一意的な解を持つことは知られている。
が滑らかな境界を持つ有界領域の場合に、
この境界値問題が一意的な解を持つことは知られている。
![]() が (円盤とか、長方形とか) 特別な形をしている場合に、
解
が (円盤とか、長方形とか) 特別な形をしている場合に、
解 ![]() を求める公式はいくつか知られているが、
ここでは多くの場合に使える数値解法を紹介する。
一見素朴であるが、多くの場合に良好な近似解を得ることが出来る。
を求める公式はいくつか知られているが、
ここでは多くの場合に使える数値解法を紹介する。
一見素朴であるが、多くの場合に良好な近似解を得ることが出来る。
![]() の外部に
の外部に![]() を「囲むように」点
を「囲むように」点
![]() を取り、
を取り、
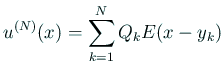
とおく (もちろん、
が成り立つ。 もし
を満たすように
が成り立つことが期待できる。この近似解法を、 the method of fundamental solutions (基本解の方法, fundamental solution method), あるいは代用電荷法 (charge simulation method) と呼ぶ7。
次のような利点がある。
が成り立つ (この場合は、差分法や有限要素法と比較して、 高精度の解が少ない計算量で得られる)。
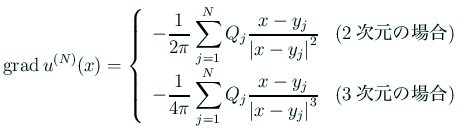
のように
基本解の方法以外に、基本解を利用する方法として、 境界要素法 (boundary element method, BEM) がある。
桂田 祐史