Next: 4.5 (細かい話) 多重連結領域の場合 Up: 4 領域の等角写像, Riemannの写像定理, ポテンシャル問題との関係 Previous: 4.3 単連結領域の場合の等角写像の正規化条件
典型的な単連結領域に Jordan 領域がある。
| Jordan曲線定理 |
|
|
この定理で存在が保証される領域を、![]() の定める Jordan 領域と呼ぶ。
Jordan領域
の定める Jordan 領域と呼ぶ。
Jordan領域 ![]() は単連結領域であるから、
Riemannの写像定理によって、
は単連結領域であるから、
Riemannの写像定理によって、![]() の等角写像
の等角写像 ![]() が存在するが、
以下に示すように、
が存在するが、
以下に示すように、
![]() は、あるポテンシャル問題を解くことによって求めることが出来る。
は、あるポテンシャル問題を解くことによって求めることが出来る。
このとき、
![]() が双正則写像で、
(4.1) を満たすとしよう。
が双正則写像で、
(4.1) を満たすとしよう。
![]() の閉包から閉円盤への同相写像
の閉包から閉円盤への同相写像
![]() に
拡張できる (Carathéodory の定理)。
以下
に
拡張できる (Carathéodory の定理)。
以下
![]() のことも
のことも ![]() と書くことにする。
と書くことにする。
関数
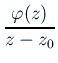 は
は ![]() で正則であり、
かつ 0
という値を取らない。
で正則であり、
かつ 0
という値を取らない。
![]() が単連結であるから、
が単連結であるから、
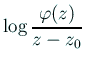 の一価正則
な分枝が取れる。
その実部、虚部をそれぞれ
の一価正則
な分枝が取れる。
その実部、虚部をそれぞれ ![]() ,
, ![]() とおく:
とおく:
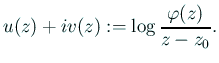
両辺の実部を取ると、
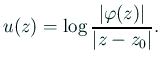
(4.3), (A.13) は、
Laplace 方程式の Dirichlet 境界値問題である。
これを解いて ![]() を求め、
を求め、![]() を
を ![]() の共役調和関数で、
の共役調和関数で、
![]() を満たすものとすると、
を満たすものとすると、![]() は次のように求まる。
は次のように求まる。
桂田 祐史