Next: 参考文献 Up: A. Poisson 方程式に対する差分法 Previous: A..5 結び
![]() は、
複素平面内の滑らかな Jordan 曲線
は、
複素平面内の滑らかな Jordan 曲線 ![]() で囲まれた Jordan 領域とする。
任意に選んだ
で囲まれた Jordan 領域とする。
任意に選んだ
![]() に対して、
Riemann の写像定理により、
に対して、
Riemann の写像定理により、
![]() を単位円板領域
を単位円板領域
![]() の上に写す等角写像
の上に写す等角写像
![]() で、
で、
![]() は、
は、
![]() から
から
![]() の上への同相写像に拡張される
(Carathéodory の定理)。
の上への同相写像に拡張される
(Carathéodory の定理)。
関数
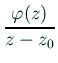 (ただし
(ただし ![]() では
では
![]() という値を取ると考える)
は
という値を取ると考える)
は
![]() 上の関数として定義されて、
上の関数として定義されて、
![]() で正則であり、0
にはならない。
で正則であり、0
にはならない。![]() は単連結であるから、
正則関数
は単連結であるから、
正則関数
![]() が存在して、
が存在して、
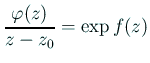
すなわち
![]() ,
,
![]() とおく。
とおく。
![]() が成り立つ。
が成り立つ。
![]() に対して、
に対して、
![]() であるから、
であるから、
ゆえに (
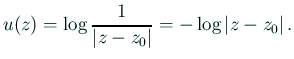
以上より、![]() は Laplace 方程式の Dirichlet 境界値問題
は Laplace 方程式の Dirichlet 境界値問題
| (A.21) |
| (A.22) |
桂田 祐史