Next: 4.3 有限要素法, FreeFem++ Up: 4 ポテンシャル問題の有限要素法による数値計算 (しばらく工事中) Previous: 4.1 ポテンシャル問題とは
![]() を
を
![]() の有界な領域、
その境界
の有界な領域、
その境界 ![]() が
が ![]() ,
, ![]() に分かれているとする。
に分かれているとする。
また領域
![]() ,
,
![]() ,
,
![]() が与えられたとき、
が与えられたとき、
注:
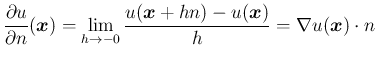 .
.
この問題は、次のように変形できる (弱定式化, weak formulation)。
|
Find
ここで
(念のため: |
条件 (6) を弱形式と呼ぶ。
適当な条件のもとで、
弱形式を満たす
![]() は一意に定まり、
それがもとの問題の解となる。
弱形式を満たす
は一意に定まり、
それがもとの問題の解となる。
弱形式を満たす ![]() を求めることでもとの問題を解く方法を
弱解の方法と呼ぶ。
(そのルーツとして有名なのは、
Riemann による写像定理の、Dirichlet の原理を用いた証明である
-- 後日説明する。)
を求めることでもとの問題を解く方法を
弱解の方法と呼ぶ。
(そのルーツとして有名なのは、
Riemann による写像定理の、Dirichlet の原理を用いた証明である
-- 後日説明する。)
桂田 祐史