- §2の (1) 「発展系の数値解析」 の 1, 2, 3 節を読む。
- §2の(2) (a)
heat1d-e-glsc.cは 3節の差分方程式を計算して、
熱方程式の初期値境界値問題 (テキストの5課のものに相当) を解くプログラム
である。コンパイル&実行してみること (もしこれが出来なかった場合は、
Mac を持って桂田のところに来ること、出来るようにしてあげます)。
これを解読する (確かに3節で説明してある計算をしていることを読み取る) こと。
- 「発展系の数値解析」の4節を、コンピューターで再現しながら読む。
そのためには、§2 の (2) の (b) heat1d-i-glsc.c,
(c) heat1n-i-glsc.c を用いる。
- Dirichlet 条件の問題を解くには heat1d-i-glsc.c
- Neumann 条件の問題を解くには heat1n-i-glsc.c
- 入力パラメーターは、
「発展系の数値解析」図の中に書いてあるので難しくないはず。
- 「発展系の数値解析」の5節を読む。
θ法というのを説明してあるが、
それを実装したプログラムが heat1d-i-glsc.c である。
プログラムを読んで、そのことを理解すること。
- heat1d-i-glsc.c の中で、連立1次方程式
(「発展系の数値解析」の p. 16 式 (46)) を解くのに、
trilu(), trisol() という関数を使っているが、
これは係数行列を LU 分解して解いている。
LU分解とは何かについては1、
§2の (4) 「発展系の数値解析の続き」に書いてあるが、
(短時間に自力で理解するのは大変と思われるので)
とりあえず「これで連立1次方程式を解いているらしい」でパスしても構わない。
- Neumann 境界条件
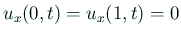 の問題をどう解くかは、
「発展系の数値解析」には書いてない。
§2の (3)「熱方程式に対する差分法 I」第1章に詳しく書いてある。
heat1n-i-glsc.c はそれを実装したものである。
輪講のテキスト [1] 第7課の問題の境界条件は、
の問題をどう解くかは、
「発展系の数値解析」には書いてない。
§2の (3)「熱方程式に対する差分法 I」第1章に詳しく書いてある。
heat1n-i-glsc.c はそれを実装したものである。
輪講のテキスト [1] 第7課の問題の境界条件は、
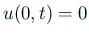 ,
,
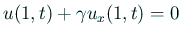 で、
この第2の方程式をどう扱うかも「熱方程式に対する差分法 I」第1章には書いてある。
これを解くためのプログラムは自分で作る必要があるが、
heat1d-i-glsc.c をたたき台にすれば、比較的容易である
(分かってしまえば数行書き換えるだけ)。
で、
この第2の方程式をどう扱うかも「熱方程式に対する差分法 I」第1章には書いてある。
これを解くためのプログラムは自分で作る必要があるが、
heat1d-i-glsc.c をたたき台にすれば、比較的容易である
(分かってしまえば数行書き換えるだけ)。
桂田 祐史
2020-01-20