勉強する場合、
以下の資料をすべて印刷することを勧める。
(2) のプログラムに関しては、
自分の Mac にダウンロードすること
(ブラウザで Ctrl-クリックして、名前をつけて保存する)。
- (1)
- 桂田「発展系の数値解析」
差分法入門。熱方程式の初期値境界値問題
(今のテキストの第5課の問題) を題材にして説明してある。
- (2)
- 現象数理学科 Mac の cglsc コマンドでコンパイル出来るプログラム
- heat1d-e-glsc.c
同次 Dirichlet 条件
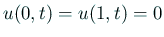 の場合、
陽解法のプログラム
(もっとも基本的、短いので読んで理解しやすい)。「発展系の数値解析」3節
の場合、
陽解法のプログラム
(もっとも基本的、短いので読んで理解しやすい)。「発展系の数値解析」3節
- heat1d-i-glsc.c
同次 Dirichlet 条件
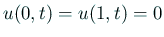 の場合、
陰解法 (θ法) のプログラム。「発展系の数値解析」5節(3)
の場合、
陰解法 (θ法) のプログラム。「発展系の数値解析」5節(3)
- heat1n-i-glsc.c
同次 Neumann 条件
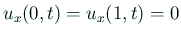 の場合、
陰解法 (θ法)のプログラム。「熱方程式に対する差分法 I」1章
の場合、
陰解法 (θ法)のプログラム。「熱方程式に対する差分法 I」1章
- (3)
- 桂田「熱方程式に対する差分法 I」第1章
同次 Dirichlet 境界条件
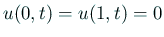 以外の境界条件の問題を
解くためにどうすれば良いか、解説してある。
以外の境界条件の問題を
解くためにどうすれば良いか、解説してある。
- (4)
- 桂田 「発展系の数値解析の続き」
連立1次方程式を解くためのLU分解の説明を詳しく書いてある。
- (5)
- その後、「熱方程式に対する差分法 I」
の続きや、
「熱方程式に対する差分法 II」
の興味があるところを読む。
桂田 祐史
2020-01-20