Next: гҒ®е ҙеҗҲ Up: Laplacian гҒЁжҘөеә§жЁҷ Previous: 6.0.0.1 иЁјжҳҺ
(е·ҘдәӢдёӯ)
![]() гҒ«еҜҫгҒ—гҒҰгҖҒ
гҒ«еҜҫгҒ—гҒҰгҖҒ
| (7) | |||
| (8) |
зӢ¬з«ӢеӨүж•° ![]() ,
, ![]() ,
, ![]() гҒ®
гҒ® ![]() ж¬ЎеҗҢж¬ЎеӨҡй …ејҸ
ж¬ЎеҗҢж¬ЎеӨҡй …ејҸ
![]() гҒҜгҖҒ
гҒҜгҖҒ![]() ж¬ЎеҗҢж¬ЎжҖ§гҒ®е®ҡзҫ©гҒӢгӮү
ж¬ЎеҗҢж¬ЎжҖ§гҒ®е®ҡзҫ©гҒӢгӮү
![\begin{jdefinition}[дҪ“зҗғиӘҝе’Ңй–ўж•°гҖҒзҗғйқўиӘҝе’Ңй–ўж•°]
$k$\ ж¬ЎеҗҢж¬ЎеӨҡй...
...c function},
\textbf{surface harmonic function})
гҒЁе‘јгҒ¶гҖӮ
\end{jdefinition}](img233.png)
|
![]() гҒҢ
гҒҢ ![]() ж¬ЎгҒ®дҪ“зҗғиӘҝе’Ңй–ўж•°гҒЁгҒҷгӮӢгҒЁгҒҚгҖҒ
ж¬ЎгҒ®дҪ“зҗғиӘҝе’Ңй–ўж•°гҒЁгҒҷгӮӢгҒЁгҒҚгҖҒ
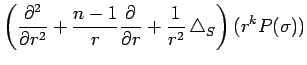 |
|||
е®ҹгҒҜгҖҒзҗғйқўдёҠгҒ® Laplace-Beltrami дҪңз”Ёзҙ гҒ®еӣәжңүеҖӨгҒЁеӣәжңүй–ўж•°гҒҜгҖҒгҒҷгҒ№гҒҰдёҠ
гҒ®еҪўгҒ§жұӮгҒҫгӮӢгҖӮ(гҒӨгҒҫгӮҠгҖҒ
![]() гҒҢеӣәжңүеҖӨгҒ®е…ЁдҪ“гҒ§
гҒӮгӮҠгҖҒеҜҫеҝңгҒҷгӮӢеӣәжңүй–ўж•°гҒҜзҗғйқўиӘҝе’Ңй–ўж•°гҒ«еҸ–гӮӢгҒ“гҒЁгҒҢеҮәжқҘгӮӢгҖӮ)
гҒҢеӣәжңүеҖӨгҒ®е…ЁдҪ“гҒ§
гҒӮгӮҠгҖҒеҜҫеҝңгҒҷгӮӢеӣәжңүй–ўж•°гҒҜзҗғйқўиӘҝе’Ңй–ўж•°гҒ«еҸ–гӮӢгҒ“гҒЁгҒҢеҮәжқҘгӮӢгҖӮ)