Next: I..2 高橋 [1] の記述を検討する Up: I. 微分多項式についての注意 Previous: I. 微分多項式についての注意
定数係数線形常微分方程式
微分作用素
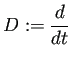 |
(I.1) |
| (I.2) |
| (I.3) |
簡単のため、2階微分方程式の場合、
微分多項式を扱っている常微分方程式のテキスト・解説はたくさんあるけれど、
この記号がどのように使われるか、典型例を一つあげてみよう。
|
|
これを見ると
![]() としているように思われるので、
解釈 (i) が有望そうであるが、それを
としているように思われるので、
解釈 (i) が有望そうであるが、それを ![]() に等しいとしているので、
に等しいとしているので、
![]() とみなしているようでもある。
とみなしているようでもある。
どのように定義するかは、正しい答えが一つだけある、 というのではないことに注意しよう。 数学の概念の多くは、複数の仕方で定義することが出来て、 ある流儀で定義したとき、 別の流儀の定義に現れる式が定理となったりする。 全体として同じことができれば構わない。