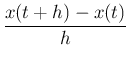

Next: 2.2.2 後退 Euler 法
Up: 2.2 簡単な数値解法
Previous: 2.2 簡単な数値解法
微分係数 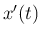 を前進差分商
を前進差分商
で近似して作った漸化式
で
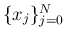 を計算する。
を計算する。
数学のどこにでも出て来る巨人 Leonhard Euler (1707-1783,
スイスの Basel に生まれ、ロシアの St Petersburg にて没する) による。


Next: 2.2.2 後退 Euler 法
Up: 2.2 簡単な数値解法
Previous: 2.2 簡単な数値解法
桂田 祐史
2015-05-30
![]() を前進差分商
を前進差分商