Next: 6.2 正方形板のChladni図形 Up: 6 固有値問題 Previous: 6 固有値問題
最初に重要なことを書く。
長方形領域
![]() で、Dirichlet条件、
Neumann境界条件下のLaplacianの固有値問題を数値計算で解く意味はほとんどない。
で、Dirichlet条件、
Neumann境界条件下のLaplacianの固有値問題を数値計算で解く意味はほとんどない。
厳密解はもちろん (有名で、多くのテキストに載っている)、 差分法で近似した場合の固有関数・固有値も簡単な式で求まるためである。
特に固有関数は、微分作用素のそれと一致する。
実を言うと、私はそのことに気づかず、 学部卒研の課題として与えてしまったことがある。 「先生、誤差がほとんど0です。」という (本当は当たり前だけれど、 そのときの私には) 驚愕の報告があって大騒ぎだった。20年以上前の笑い話。
まとめたものを書いたっけ??
というわけで Laplacian (Laplace作用素) の固有値問題を差分法で解くのは今ひとつ面白みがない (もちろん複雑な形状の領域を持ってくれば難しくなるが、 今度は逆に難しすぎる)。
少し唐突かもしれないが、
重調和作用素
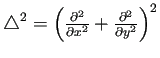 の場合が面白い。
実は私のゼミで、卒研や修士論文のテーマで取り組んだ人が何人かいる。
これはいわゆる Chladni 図形 (クラドニ図形)
のシミュレーションとみなすことが出来る。
長方形領域でもそんなに簡単ではない。
テキストによっては “単純支持” という境界条件を与えて、
変数分離で厳密解を求めてしまっているものがあるが、
より自然な設定である (だから重要と考えられる) free edge の場合は、
変数分離がうまくいかず、
境界条件の方程式がかなり複雑になり、
差分法のプログラムを書くのも一苦労する。
でもなんとか出来た、と言うのが以下の平野さんの修論である
(係数行列の導出に半年近くかかったという力作)。
の場合が面白い。
実は私のゼミで、卒研や修士論文のテーマで取り組んだ人が何人かいる。
これはいわゆる Chladni 図形 (クラドニ図形)
のシミュレーションとみなすことが出来る。
長方形領域でもそんなに簡単ではない。
テキストによっては “単純支持” という境界条件を与えて、
変数分離で厳密解を求めてしまっているものがあるが、
より自然な設定である (だから重要と考えられる) free edge の場合は、
変数分離がうまくいかず、
境界条件の方程式がかなり複雑になり、
差分法のプログラムを書くのも一苦労する。
でもなんとか出来た、と言うのが以下の平野さんの修論である
(係数行列の導出に半年近くかかったという力作)。
一方、この Chladni 図形の問題は、 Ritzの方法で有名な Walter Ritz の記念碑的な論文 [5] で、 数値計算により解かれたことで有名である (コンピューターのない時代の、ほとんど神話のような出来事)。 その方法は有限要素法の基礎にもなっている。 固有値問題の数値計算には有限要素法がおすすめである。 正多角形板の Chladni 図形は古くから色々実験的に調べられてきたが、 それについて有限要素法でシミュレーションしたのが以下の遠藤さんの修論である。
(間にもう一人いるのだけれど、公開承諾をもらい損ねたような記憶が… 失敗したなあ。)