Next: 3 Briggs の方法 Up: 2 Napier Previous: 2.1 人となりと業績
小数が普及していない時代なので、
なるべく小数が現れないように工夫されている。
![]() とおいて、
とおいて、
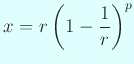
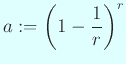
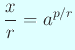
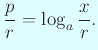
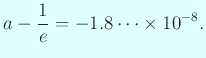
便宜上
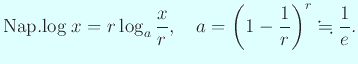
| Napierの対数を現代の対数で表す |
|
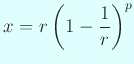
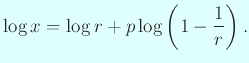
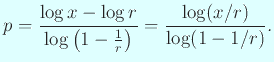
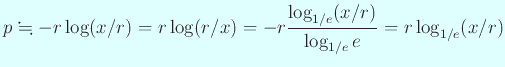
|
![]() を
を ![]() に選んだのは、
彼が利用できる最良の正弦表が 7 桁のものであった事実に基づいている。
に選んだのは、
彼が利用できる最良の正弦表が 7 桁のものであった事実に基づいている。
![]() として
として
![]() という形をしている数を選んだ。
という形をしている数を選んだ。
序文の中で彼の発見の背後の考察について説明しているとか。
Seeing there is nothing (right well-beloved Students of the Mathematics) that is so troublesome to mathematical practice, nor that doth more molest and hinder calculators, than the multiplications, divisions, square and cubical extractions of great numbers, which besides the tedious expense of time are for the most part subject to many slippery errors, I began therefore to consider in my mind by what certain and ready art I might remove those hindrances. And having thought upon many things to this purpose, I found at length some excellent brief rules to be treated of (perhaps) hereafter. But amongst all, none more profitable than this which together with the hard and tedious multiplications, divisions, and extractions of roots, doth also cast away from the work itself even the very numbers themselves that are to be multiplied, divided and resolved into roots, and putteth other numbers in their place which perform as much as they can do, only by addition and subtraction, division by two or division by three.
しばしば Napier の対数は ![]() を底とする (“they are to base
を底とする (“they are to base ![]() ”)
と言われるのは理由のないことではないが、誤解を招きやすい説明である。
Napier の時代には代数が十分発展していなかったので、
”)
と言われるのは理由のないことではないが、誤解を招きやすい説明である。
Napier の時代には代数が十分発展していなかったので、
![]() とならないことは不便であった。
とならないことは不便であった。
![]() となるような対数の導入は
Napier と Briggs の議論の中で現れたという
(初めて出版されたのは Briggs の著書の中である)。
となるような対数の導入は
Napier と Briggs の議論の中で現れたという
(初めて出版されたのは Briggs の著書の中である)。
Briggs は Napier の 1614 年のラテン語テキストを読み、 1615年に London から Edinburgh に旅をした (現在ならば列車で4時間の行程だが、 馬で4日かかったという)。
彼らの会合の様子は次のようであったという。
Mr Briggs appoints a certain day when to meet at Edinburgh; but failing thereof, Merchiston was fearful he would not come. It happened one day as John Marr and the Lord Napier were speaking of Mr Briggs, “Oh! John,” saith Merchiston, “Mr Briggs will not come now”; at the very instant one knocks at the gate, John Marr hastened down and it proved to be Mr Briggs to his great contentment. He brings Mr Briggs into my Lord's chamber, where almost one quarter of an hour was spent, each beholding other with admiration, before one word was spoken. At last Mr Briggs began, -”My Lord, I have undertaken this long journey purposely to see your person, and to know by what engine of wit or ingenuity you came first to think of this most excellent help unto astronomy, viz. the Logarithms ...
Briggs は会う前に送った手紙の中で、対数は ![]() を底とするべきだと
提言し、数表の作成に着手していた。
Napier は彼も同じアイディアを持っていたが、
健康を害していることや他の重大な理由から、
新しい数表の作成を請け合うことはできないと答えた。
を底とするべきだと
提言し、数表の作成に着手していた。
Napier は彼も同じアイディアを持っていたが、
健康を害していることや他の重大な理由から、
新しい数表の作成を請け合うことはできないと答えた。
Napier は Briggs に、
新しい数表は底を 10 として、![]() となるように作るべきだと提案したが、
実際に Briggs はそのような数表を作成した。
Briggs は Napier と一ヶ月一緒にすごし、
1616年の二度目の訪問をして、
1617年夏の三度目の訪問の前に Napier は亡くなった。
となるように作るべきだと提案したが、
実際に Briggs はそのような数表を作成した。
Briggs は Napier と一ヶ月一緒にすごし、
1616年の二度目の訪問をして、
1617年夏の三度目の訪問の前に Napier は亡くなった。
200年後の Laplace の言葉
1620年 Edmund Gunter (1581-1626) により、 ガンター尺 (Gunter's scale) が作成された。 計算尺の走り。
三角関数表を使って積と商を計算することが行われていたのが
G A Gibson, Napier and the invention of logarithms, in E M Horsburgh (ed.), Napier Tercentenary Celebration : Handbook of the exhibition (Edinburgh, 1914), 1-16.
![\includegraphics[width=8cm]{Napier/Napier.eps}](img77.png)
桂田 祐史