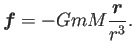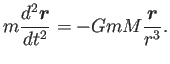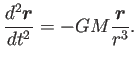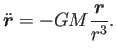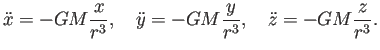万有引力 (universal gravitation) の大きさは
ただし、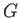 は万有引力定数と呼ばれる正定数である。SI 単位系で
は万有引力定数と呼ばれる正定数である。SI 単位系で
ここでは太陽は静止しているとする。
という説明に何の疑問も抱かない学生が多い。うーん。
二つの言い訳がある。
- 太陽は惑星と比べて質量が大きいので、太陽の動きは無視できる。
(太陽の質量は、地球の質量の 33 万倍で、共有重心は太陽の中)
- 共有重心のまわりの運動とすれば…
地球が受ける力
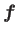 は、
は、
運動方程式に代入して
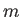 で割って
で割って
以下、関数の時間微分を  をつけて表すことにする。
をつけて表すことにする。
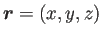 と成分表示すれば、
と成分表示すれば、
初期時刻 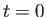 における惑星の位置ベクトル
における惑星の位置ベクトル
とする。また速度ベクトルを
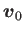 とする。
初期条件は
とする。
初期条件は
桂田 祐史
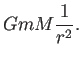
![]() は、
は、