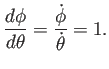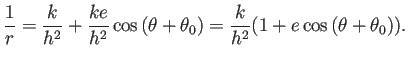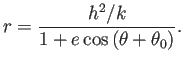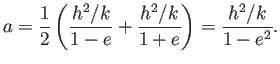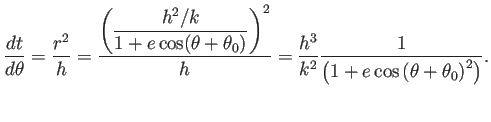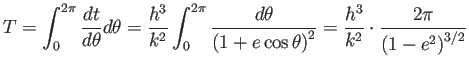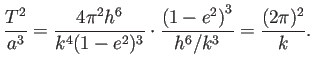G. 高野 [5] 第1章 §2 から
藤田先生とは少し異なったやり方で Kepler の法則を証明している。
周期の計算がしてあるところが参考になる。
から
第2式の両辺に左から
 をかけることで、
をかけることで、
|
(16) |
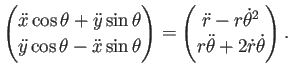 |
この等式は、物理と関係無く一般に成り立つことを注意しておく。
思いの外簡単になった気がするが、多分、
動径方向の加速度と接線方向の加速度を計算しているせいだと思う
(それが極座標で簡単になるのは自然であろう)。
さらに、ここで
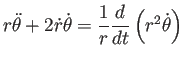 であることも注意しておく
(面積速度
であることも注意しておく
(面積速度
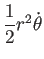 が顔を出す)。
が顔を出す)。
万有引力の法則
を仮定すると
が得られるので (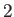 つ目が 0 になるのは、
万有引力がいわゆる中心力であるからである)、
(16) に代入して
つ目が 0 になるのは、
万有引力がいわゆる中心力であるからである)、
(16) に代入して
|
(17) |
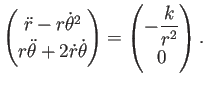 |
新しい従属変数
|
(18) |
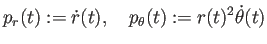 |
を導入すると、
であるから、 (17) は次と同値である。
|
(19) |
![$\displaystyle \frac{\D}{\D t} \begin{pmatrix}r p_r \theta p_\theta \end...
...3}-\dfrac{k}{r^2} [2ex] \dfrac{p_\theta}{r^2} [1ex] 0 \end{array} \right).$](img280.png) |
このうち
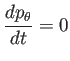 より
より
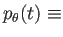 const.
const.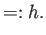
さて、
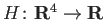 を
を
で定めるとき (この式の 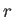 ,
, 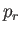 ,
, 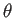 ,
, 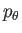 は独立変数である)、
は独立変数である)、
であるから、(19) は次と同値である。
(注: いずれの方程式も右辺は
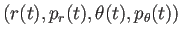 での値)
での値)
要するにいわゆる Hamilton 系である。すると、
であるから、
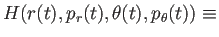 const.
const.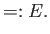
(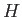 を定義してから、このエネルギー保存則を導くまでは、率直に言って、
衒学的な気がする?いや、そもそも、あの従属変数の導入は、
Hamilton系であることから来たものだ。)
を定義してから、このエネルギー保存則を導くまでは、率直に言って、
衒学的な気がする?いや、そもそも、あの従属変数の導入は、
Hamilton系であることから来たものだ。)
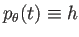 を代入すると
を代入すると
これを
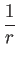 と
と 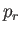 の関係と見て整理すると、
の関係と見て整理すると、
( ) ) |
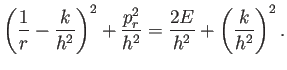 |
以下、 は
は
|
(20) |
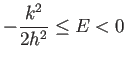 |
を満たすと仮定する。左の不等式から (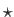 ) の右辺は非負である。すると
この右辺は
) の右辺は非負である。すると
この右辺は
ただし
と書ける。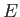 についての仮定から、
についての仮定から、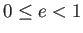 である。
である。
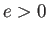 のとき、(
のとき、(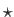 ) は
) は
と同値である。ゆえに連続関数
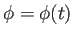 が存在して、
が存在して、
(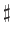 ) ) |
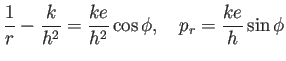 |
となる。この式は  のときも成立する。
第1式を微分して、
のときも成立する。
第1式を微分して、
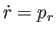 を用いると、
を用いると、
左辺に ( ) の第2式を代入して
) の第2式を代入して
整理して
一方、
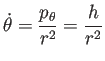 であるから、
であるから、
ゆえに
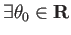 s.t.
s.t.
(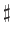 ) の第1式に代入して
) の第1式に代入して
ゆえに
これから軌跡は原点を一つの焦点とする楕円である。
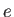 は離心率で、楕円の長径を
は離心率で、楕円の長径を 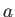 とすると、
とすると、
ここで
であるから、周期を 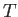 とすると、
とすると、
(最後の等式は、微積でも解けるが、複素関数論ネタかも知れない。)
これから Kepler の第3法則が得られる:
桂田 祐史
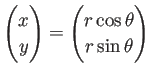
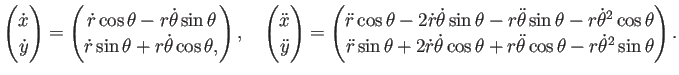
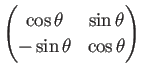 をかけることで、
をかけることで、
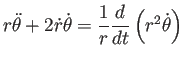 であることも注意しておく
(面積速度
であることも注意しておく
(面積速度
![]() が顔を出す)。
が顔を出す)。
![$\displaystyle \begin{pmatrix}\ddot x \ddot y\end{pmatrix} = - \begin{pmatrix}\dfrac{kx}{r^3} [1.5ex] \dfrac{ky}{r^3} \end{pmatrix}$](img266.png)
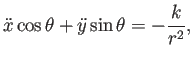
![$\displaystyle =\frac{\D^2 r}{\D t^2} =\left[ \frac{\D^2r}{\D t^2}-r\left(\frac{...
...^2} \right] +\frac{1}{r^3}\left(r^2\frac{\D\theta}{\D t}\right)^2-\frac{k}{r^2}$](img274.png)
![$\displaystyle =\left[ \frac{\D^2r}{\D t^2}-r\left(\frac{\D\theta}{\D t}\right)^2+\frac{k}{r^2} \right] +\frac{p_\theta^2}{r^3}-\frac{k}{r^2},$](img275.png)
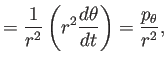
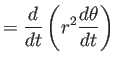
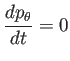 より
より
![]() を
を
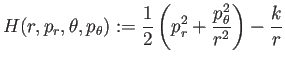
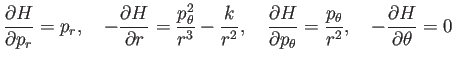
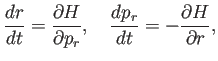
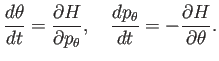
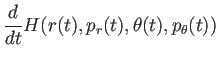
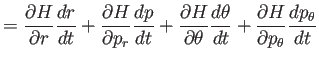
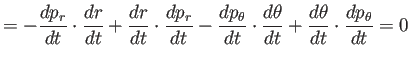
![]() を代入すると
を代入すると
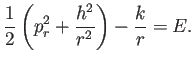
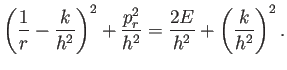
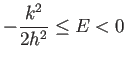
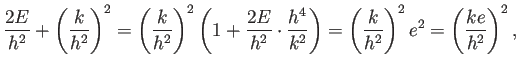
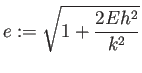
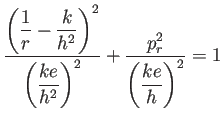
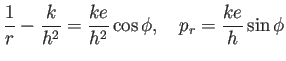
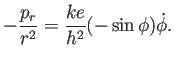
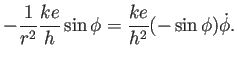
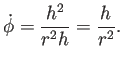
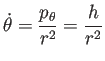 であるから、
であるから、