Next: 3 2次元の問題 Up: 2.4 課題 Previous: 2.4 課題
| (8) | 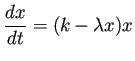 | |
| (9) |
![]() のとき、解は次式で与えられる。
のとき、解は次式で与えられる。
| (10) | 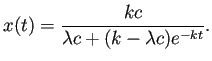 |
以前、資料調べをしたことがあった (原典中心なので、
現代的な解説は微分方程式の教科書的な本を当たると良いだろう)。
「マルサスの法則, フェルフルストのロジスティック方程式, ロトカ・ヴォルテラの方程式」
平衡点やその安定性を調べることを勧める。 (用語の定義は、付録 D, D.3, D.3 を見よ。 そこに載っている定理で安定性の判定が可能であるが、 この場合は解が得られているので、それから安定性を判定することもできる。)