Next: C. гҒқгҒ®д»– Up: Banach з©әй–“гҒ«гҒҠгҒ‘гӮӢеҫ®з©ҚеҲҶгҒ®еҹәжң¬е®ҡзҗҶ Previous: A. е®®еҜә [2] гҒӢгӮү
е‘ҪйЎҢ 4.2 гҒҜеҹәжң¬зҡ„гҒӘеҶ…е®№гҒ гҒҢгҖҒ жЎҲеӨ–гҒЁијүгҒЈгҒҰгҒ„гҒӘгҒ„жң¬гҒҢеӨҡгҒ„гҒ®гҒ§гҖҒ Brezis [4] гҒ«еҫ“гҒЈгҒҰиЁјжҳҺгҒ—гҒҰгҒҠгҒҸгҖӮ

|
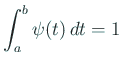
гӮ’жәҖгҒҹгҒҷ
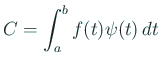 гҒЁгҒӘгӮӢ)гҖӮ
д»»ж„ҸгҒ®
гҒЁгҒӘгӮӢ)гҖӮ
д»»ж„ҸгҒ®
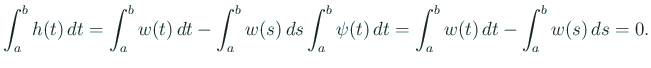
гӮҶгҒҲгҒ«
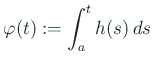
гҒЁгҒҠгҒҸгҒЁ
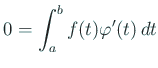
гҒ§гҒӮгӮӢгҖӮ гҒ“гӮҢгҒ«
| 0 | 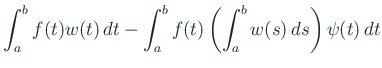 | ||
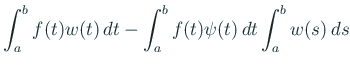 | |||
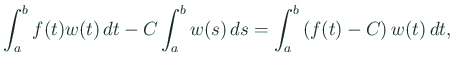 |
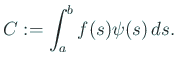
еӨүеҲҶжі•гҒ®еҹәжң¬иЈңйЎҢгҒӢгӮү

|
 |
 | ||
 | |||
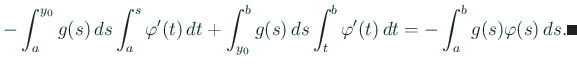 |
е‘ҪйЎҢ 4.2гҒ®иЁјжҳҺ
![]() гҒЁгҒҷгӮӢгҖӮ
гҒЁгҒҷгӮӢгҖӮ
![]() гӮҲгӮҠ
гӮҲгӮҠ
![]() гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
д»»ж„ҸгҒ«
гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
д»»ж„ҸгҒ« ![]() гӮ’еҸ–гҒЈгҒҰеӣәе®ҡгҒ—гҒҰгҖҒ
гӮ’еҸ–гҒЈгҒҰеӣәе®ҡгҒ—гҒҰгҖҒ
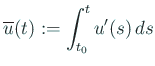
гҒЁгҒҠгҒҸгҒЁ
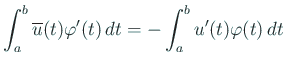
дёҖж–№
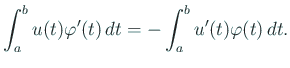
гҒ“гӮҢгҒӢгӮү
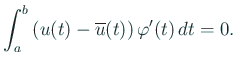
иЈңйЎҢB.1гӮҲгӮҠ
гҒқгҒ“гҒ§
гҒЁгҒҠгҒҸгҒЁгҖҒ
гҒқгҒ—гҒҰ
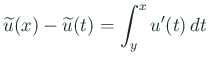
жЎӮз”° зҘҗеҸІ