Next: B. 命題 4.2 の証明 Up: Banach 空間における微積分の基本定理 Previous: 4.2 Banach 空間に値を持つ関数の場合
![\begin{jtheorem}
X は Banach 空間、
$x\colon[a,b]\to X$\ は Bochner 可積...
...laymath}
y'(t)=x(t)\quad\mbox{a.e. on $[a,b]$}.
\end{displaymath}\end{jtheorem}](img64.gif)
|
ところで (実数値関数と異なり) Banach 空間値関数
![]() は
絶対連続であるというだけでは、
ほとんど到るところ微分できるとは限らない。
しかし次の定理が成り立つ。
は
絶対連続であるというだけでは、
ほとんど到るところ微分できるとは限らない。
しかし次の定理が成り立つ。
![\begin{jtheorem}
$X$\ は Banach 空間、
$y\colon[a,b]\to X$\ は絶対連続...
...laymath}
y'(t)=x(t)\quad\mbox{a.e. on $[a,b]$}.
\end{displaymath}\end{jtheorem}](img66.gif)
|
|
|
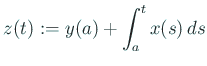
は定理 A.1 より 絶対連続かつほとんど到るところ強微分可能な 関数で、
を仮定するとに対して
は絶対連続である (
の弱連続性)
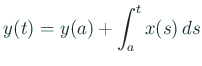
なお
![\begin{jtheorem}
$X$\ は回帰的 Banach 空間、$y\colon[a,b]\to X$\ は絶�...
...a)+\int_a^t x(s)\,\D s\quad\mbox{($t\in[a,b]$)}.
\end{displaymath}\end{jtheorem}](img76.gif)
|
![\begin{jcorollary}
$X$\ は回帰的 Banach 空間、$y\colon[a,b]\to X$\ と�...
...laymath}
y'(t)=x(t)\quad\mbox{a.e. on [a,b]}.
\end{displaymath}\end{jcorollary}](img77.gif)
|
桂田 祐史