Next: 3. の内積 Up: 2. の内積と親しもう Previous: 2.11 直交射影作用素
![\begin{jtheorem}[Riesz の表現定理 (Riesz representation theorem)]
$f$\ を...
...(x,a)\quad\mbox{($x\in\R^n$)}
\end{displaymath}が成り立つ。
\end{jtheorem}](img36.gif)
|
以上が Riesz の表現定理 (の ![]() 版) だが、
率直に言って、
この定理は
版) だが、
率直に言って、
この定理は ![]() で考えると明らかすぎてアホらしい。
実際、
で考えると明らかすぎてアホらしい。
実際、
![]() とすると、
とすると、
ということだから、
と、
![]() は平面
は平面
![]() の法線ベクトルであることに注意しよう。
射影定理を使えば
の法線ベクトルであることに注意しよう。
射影定理を使えば ![]() の法線ベクトル
の法線ベクトル ![]() を作ることができる。
直感的に
を作ることができる。
直感的に ![]() と
と ![]() が平行であることがわかるので、
が平行であることがわかるので、
![]() となる
となる ![]() が存在するはずだが、
この
が存在するはずだが、
この ![]() は簡単に求まる。実際、
は簡単に求まる。実際、
![]() に
に ![]() を代入すると
を代入すると
であるから
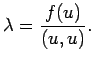
それゆえ、後は
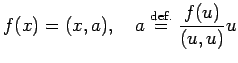
が成り立つことをチェックするだけである。
![]() の場合は明らか (
の場合は明らか (![]() でよい)。
でよい)。
![]() とする。
とする。
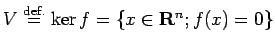
とおくと、これは
とおく。
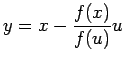
とおくと、
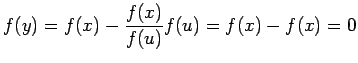
であるから
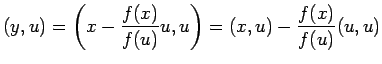
であるから、
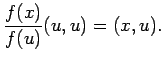
すなわち
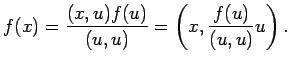
ゆえに
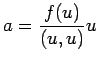
と置けばよい。
桂田 祐史