Next: 2.9 直交直和 Up: 2. の内積と親しもう Previous: 2.7 QR 分解
正規直交基底を用いて正射影の存在を証明しよう。 つまり解きかけだった例題 2 を解決することになる。
![\begin{jproposition}[正射影の存在, 射影定理 (projection theorem)]
$V$...
...}
y=\sum_{j=1}^m (x,v_j)v_j
\end{displaymath}と書ける。
\end{jproposition}](img27.gif)
|
と表わせる。これは
ということだが、(2.3) から
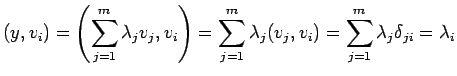
であるから
と同値である。よって、
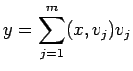
が求める直交射影である。
![]() の
の ![]() への正射影を
への正射影を ![]() とするとき、
とするとき、![]() とおくと、
とおくと、
が成り立つ。このような分解は一意的である。すなわち
とすると
実際
でこれは
と表わす (もう少していねいに!)。
桂田 祐史